01. 平面図形☆ひらめき一本勝負!(うっしー さん)
辺 AB の長さが 28/27 cm、辺 BC の長さが 10/9 cm、辺 CA の長さが 4/3 cm の三角形 ABC があります。∠A の 2 等分線を引き、∠A の 2 等分線に B から引いた垂線の足を P とします。同様に、∠C の 2 等分線を引き、∠C の 2 等分線に B から引いた垂線の足を Q とします。
このとき、線分 PQ の長さは何 cm になるでしょう。
〔解答・解説〕三角形 ABP を AP で折り返し、B が移った点を R とする。
∠BAP=∠RAP より、R は直線 AC 上にある。
折り返しているので、BP=PR…①、AB=AR=28/27 cm…②
また、三角形 CBQ を CQ で折り返し、B が移った点を S とする。
S は直線 AC 上にある。
折り返しているので、BQ=QS…③、CB=CS=10/9 cm…④
②、④より、SR=28/27+10/9-4/3=22/27 (cm)
①、③より、三角形 BRS は三角形 BPQ を相似比 2 倍に拡大したものであるから、PQ=SR÷2=11/27 (cm)
02. 三等分にしてね。(清川 育男 さん)
牛乳の入っているポットと A、B、C の 3 つの空の容器があります。ポットには 24 リットルの牛乳が入っています。A、B、C の 3 つの容器の容量はそれぞれ 13 リットル、10 リットル、7 リットルです。
ポット、A、B、C の容器を利用して、8 リットルずつ 3 等分する最小手順は 13 手です。
では、その 13 手でできる方法を解答してください。
〔解答・解説〕変移の様子は以下のとおり。
| 手数 | ポット | A (13 L) | B (10 L) | C (7 L) | 移動 |
| 0 | 24 | 0 | 0 | 0 | |
| 1 | 11 | 13 | 0 | 0 | ポ → A |
| 2 | 11 | 3 | 10 | 0 | A → B |
| 3 | 11 | 0 | 10 | 3 | A → C |
| 4 | 0 | 11 | 10 | 3 | ポ → A |
| 5 | 0 | 13 | 8 | 3 | B → A |
| 6 | 0 | 9 | 8 | 7 | A → C |
| 7 | 7 | 9 | 8 | 0 | C → ポ |
| 8 | 7 | 2 | 8 | 7 | A → C |
| 9 | 14 | 2 | 8 | 0 | C → ポ |
| 10 | 14 | 0 | 8 | 2 | A → C |
| 11 | 1 | 13 | 8 | 2 | ポ → A |
| 12 | 1 | 8 | 8 | 7 | A → C |
| 13 | 8 | 8 | 8 | 0 | C → ポ |
なお、13 手でできる方法はこの一通りしかありません。
03. やっぱり後手有利?(キューダ さん)
4 組のペアからなる 8 枚のカードを使って、二人で神経衰弱の勝負をする事を考えます。
両者とも、「最善手」を取ったときの、(先手勝ちの確率):(引き分けの確率):(後手勝ちの確率) を最も簡単な整数の比で答えてください。ここでの「最善手」は、最終的により多くのカードが手に入るような手とします。なお、神経衰弱とは、
- カードをよくかき混ぜ、裏向きに伏せて「場」に並べます。
- 手番の人が、「場」のカードを 1 枚ずつ、2 枚めくります。表にしたカードは、相手にも見せます。
- その表にしたカードがペアだったら、この 2 枚のカードを「場」から「手元」に持ってきて自分のものにし、2. に戻ります。 ペアでなかった場合は、そのカードを再びひっくり返して裏向きにし、手番を代えて 2. に戻ります。
- 「場」のカードが全て無くなったら終了で、「手元」にあるカードの枚数が多い方が勝ちです。
の様なゲームですが、次の様な特別ルールを課します。
- 1 枚目のカードをめくる時
それまでの経過からペアになるものが分かっていれば、そのペアのカードをめくり、直ちに手に入れること。ペアになるものが無いならば、必ず未確認のカードをめくること。 - 2 枚目のカードをめくる時
1 枚目にめくったカードが、確認済みのカードのペアだったら、2 枚目のカードはそのペアのカードをめくり、直ちに手に入れること。
この条件で、2 組(4 枚)のカードで勝負を行った時の、先手勝ち、後手勝ちの確率は、それぞれ、1/3、2/3 なので、この問題の書式に従った解答は、1:0:2。3 組の場合はそれぞれ、7/15、8/15 なので、7:0:8 となります。いずれも後手番が有利ですが、やっぱり、4 組の場合も、後手有利?
〔解答・解説〕場にいくつかのカードが残っている状態からそれがなくなるまで、どのような状態へどのような確率で変移していくかを考える。
【ここで使う表記について】
[ ] 内に、手元と場のカードについての情報を以下のルールで記す。[ ] の前の数はその状態になる確率を表し、[ ] 内の先頭の+は省略する。
[(+、-) (数) (+、-) (アルファベット、?)]
- (数) とその直前の符号
手元のカードの枚数の差。
"0" のときは (場に何もない場合を除いて) 省略。
符号については、基準としている人の方が多い場合は+。 - (アルファベット、?) とその直前の符号
場に残っているカードを表し、それぞれの記号の意味は
小文字のアルファベット:うら返しになっている既知のカード
大文字のアルファベット:手番の人がめくっているカード
?:まだめくられていない未知のカード
同じアルファベット(大文字小文字は区別しない)はペア。
符号については、基準としている人に手番がある場合は+、相手に移っている場合は-とする。
各カードに対するアルファベットの割り当ては、ペア、非ペア関係が確認できる範囲で適当につけかえている。
例えば、[abA?????] は場に 8 枚のカードがあり、そのうち 2 枚はそれまでのプレイで判明していて、手番の人が 1 枚だけめくった状態を表す。そして、そのめくったカードは、判明しているカードの一つとペアである ([abA?????] と [abB?????] を同一視する)。また、両プレイヤーの手元にあるカードの枚数に差はない。
1) 場にカードが 4 枚残っていて、そのうち 2 枚が判明している状態:
[ab??]=[4]
2) 場にカードが 4 枚残っていて、そのうち 1 枚が判明している状態:
[a???]=1/3[aA??]+2/3[aB??]
=1/3[4]+2/3×(1/2[aBB?]+1/2[aBA?])
=1/3[4]+2/3×(1/2[4]+1/2[-4])
=2/3[4]+1/3[-4]
ここで、[aB??] のあと、既知のカードをめくる戦略と、未知のカードをめくる戦略が考えられるが、後者を選択する。仮に、既知のカードをめくって手番を相手に回すと、[-ab??] となり、残りすべてのカードを相手に取られてしまう。したがって、未知のカードをめくるのが最善手となる。
5) の [abC???]、9) の [abcD????] においても同様の理由でこの戦略を用いる。
3) 場にカードが 4 枚残っていて、すべて未確認の状態:
[????]=[A???]=1/3[AA??]+2/3[AB??]
=1/3[4]+2/3[-ab??]=1/3[4]+2/3[-4]
4) 場にカードが 6 枚残っていて、そのうち 3 枚が判明している状態:
[abc???]=[6]
5) 場にカードが 6 枚残っていて、そのうち 2 枚が判明している状態:
[ab????]=2/4[abA???]+2/4[abC???]
=2/4[2+a???]+2/4×(1/3[abCC??]+2/3[abCA??])
=2/4[2+a???]+2/4×(1/3[2+ab??]+2/3[-2-ab??])
=2/4×(2/3[6]+1/3[-2])+2/4×(1/3[6]+2/3[-6])
=1/2[6]+1/6[-2]+1/3[-6]
6) 場にカードが 6 枚残っていて、そのうち 1 枚が判明している状態:
[a?????]=1/5[aA????]+4/5[aB????]
第 2 項は戦略により結果が異なる。
6-a) 未知のカードをめくる場合:
[aB????] → 1/4[aBB???]+1/4[aBA???]+2/4[aBC???]
=1/4[2+a???]+1/4[-2-a???]+2/4[-abc???]
=1/4×(2/3[6]+1/3[-2])+1/4×(2/3[-6]+1/3[2])+2/4[-6]
=1/6[6]+1/12[2]+1/12[-2]+2/3[-6]
6-b) 既知のカードをめくる場合:
[aB????] → [AB????]=[-ab????]
=1/3[6]+1/6[2]+1/2[-6]
よって、6-b) が最善手となる。
[a?????]=1/5[aA????]+4/5[aB????]
=1/5[2+????]+4/5[AB????]
=1/5×(1/3[6]+2/3[-2])+4/5×(1/3[6]+1/6[2]+1/2[-6])
=5/15[6]+2/15[2]+2/15[-2]+6/15[-6]
7) 場にカードが 6 枚残っていて、すべて未確認の状態:
[??????]=[A?????]
=1/5[AA????]+4/5[AB????]
=1/5[2+????]+4/5[AB????] ← この式は 6) と同様
=5/15[6]+2/15[2]+2/15[-2]+6/15[-6]
8) 場にカードが 8 枚残っていて、そのうち 4 枚が判明している状態:
[abcd????]=[8]
9) 場にカードが 8 枚残っていて、そのうち 3 枚が判明している状態:
[abc?????]=3/5[abcA????]+2/5[abcD????]
=3/5[2+ab????]+2/5×(1/4[abcDD???]+3/4[abcDA???])
=3/5[2+ab????]+2/5×(1/4[2+abc???]+3/4[-2-abc???])
=3/5×(1/2[8]+1/6[0]+1/3[-4])+2/5×(1/4[8]+3/4[-8])
=4/10[8]+1/10[0]+2/10[-4]+3/10[-8]
10) 場にカードが 8 枚残っていて、そのうち 2 枚が判明している状態:
[ab??????]=2/6[abA?????]+4/6[abC?????]
第 2 項は戦略により結果が異なる。
10-a) 未知のカードをめくる場合:
[abC?????]
→ 1/5[abCC????]+2/5[abCA????]+2/5[abCD????]
=1/5[2+ab????]+2/5[-2-ab????]+2/5[-8]
=1/5×(1/2[8]+1/6[0]+1/3[-4])+2/5×(1/3[4]+1/6[0]+1/2[-8])+2/5[-8]
=3/30[8]+4/30[4]+3/30[0]+2/30[-4]+18/30[-8]
10-b) 既知のカードをめくる場合:
[abC?????] → [-abc?????]
=9/30[8]+6/30[4]+3/30[0]+0/30[-4]+12/30[-8]
よって、10-b) が最善手となる。
[ab??????]=2/6[abA?????]+4/6[abC?????]
=2/6[2+a?????]+4/6[-abc?????]
=2/6×(5/15[8]+2/15[4]+2/15[0]+6/15[-4])+4/6×(3/10[8]+2/10[4]+1/10[0]+4/10[-8])
=14/45[8]+8/45[4]+5/45[0]+6/45[-4]+12/45[-8]
11) 場にカードが 8 枚残っていて、すべて未確認の状態:
[????????]=[A???????]
=1/7[AA??????]+6/7[AB??????]
=1/7[2+??????]+6/7[-ab??????]
=1/7×(5/15[8]+2/15[4]+2/15[0]+6/15[-4])+6/7×(12/45[8]+6/45[4]+5/45[0]+8/45[-4]+14/45[-8])
=29/105[8]+14/105[4]+12/105[0]+22/105[-4]+28/105[-8]
したがって、
先手勝ちの確率=29/105+14/105=43/105
引き分けの確率=12/105
後手勝ちの確率=22/105+28/105=50/105
すなわち、答えは 43:12:50 である。
04. 角度の問題(ごんごんま さん)
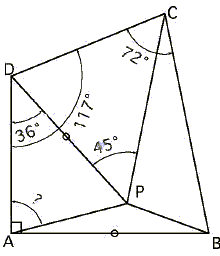
∠ADC=117 度、∠DAB=90 度、∠DCB=72 度の四角形 ABCD の内部に点 P を取ったところ、AB=DP、∠ADP=36 度、∠DPC=45 度になりました。
このとき、∠DAP は何度になるでしょうか。
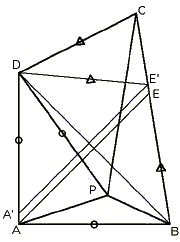
〔解答・解説〕 三角形 PDC を点 D を中心として時計回りに 36° 回転してできる三角形を三角形 A'DE' とす ると、点 E' は辺 BC 上にある。なぜなら、三角形 CDE' は頂角 36°、底角 72° の二等辺三角形 となるからである。
辺 BC 上に CD=BE となる点 E をとる。∠ABE=360-117-90-72=81°、∠A'DE'=∠PDC=117-36=81° より、∠ABE=∠A'DE'
よって、三角形 ABE と三角形 A'DE' は合同となり、AE=A'E'
∠DA'E'=∠DPC=45°、
∠DAE=90°-∠BAE=90°-∠DPC=45° より、AE//A'E'
ところが、辺 AD と辺 BC は平行ではないので、AE=A'E' となるには点 A と点 A' が一致しなければならない。よって、DA=DP
したがって、三角形 ADP は二等辺三角形となり、
∠DAP=(180-36)÷2=72°
05. 単位にまどわされるな!(長野 美光 さん)
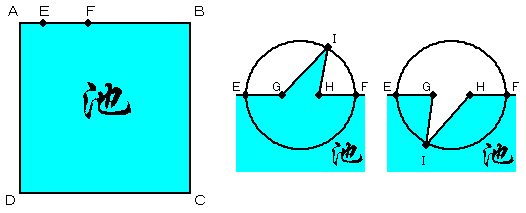
面積が 36 アールの正方形の池 ABCD があり、辺 AB の部分だけが道になっています。
いま、A 地点にヨシオ君が、B 地点にお父さんとポチがいます。ヨシオ君とお父さんは同時に道 AB をお互いに向かって移動をはじめます。ポチも、やはり同時に移動を始めますが、最初はヨシオ君に向かって進み、ヨシオ君に出会うと、引き返してお父さんに向かって進みます。ヨシオ君の速さは時速 3.6 km、お父さんの速さは分速 270 m、ポチの速さは秒速 9 m で、一定の速さで移動します。ポチが最初にヨシオ君に出会って、引き返してお父さんに出会ったときのヨシオ君の位置を E、お父さんとポチの位置を F とします。
さて、ヨシオ君のお父さんは、この池を含む広大な土地の持ち主ですが、点 E と点 F を基準にして池の形を変える計画を立てました。お父さんは、業者に
「まず、道 AB 上に、2 点 G、H をとり、これと、別の点 I を結んで、三角形 GHI をつくるのだ。ただし、2 点 G、H は、EG=GH=HF を満たしていること。また、点 I は、EF を直径とする円の円周上ならどこにとっても良い。点 I が正方形 ABCD の外側にあるときは、三角形 GHI の部分を新たに池にする。点 I が正方形 ABCD の内側にあるときは、三角形 GHI の部分は埋め立てて陸地にする。点 I が正方形 ABCD の辺上にあるときは、三角形 GHI が出来ないが、その場合は特別に池の形は変えないことにする。」
という条件を出しました。それを聞いていたヨシオ君は、点 I が正方形 ABCD の外側にあるとき、内側にあるときとして、図のような形状を思い浮かべましたが、もちろんこの他にもいろんな形状が考えられます。
さて、お父さんの出した条件を満たす池の形で、
(1) 池の面積が最小となるとき、池の面積は何 m² ですか。
(2) 池の面積が最大となるとき、池の面積は何アールですか。
道の幅、人やポチの大きさは考慮せず、線分および点と考えます。ポチが折り返すときの時間は 0 とします。1 アールは 1 辺が 10 m の正方形の面積、つまり 100 m² です。
〔解答・解説〕点 E、F の位置を求める。
池の面積は 36 a であるから、1 辺の長さは 60 m である。また、ヨシオ君とお父さんの速さはそれぞれ毎秒 1 m、毎秒 4.5 m である。
はじめ、ヨシオ君とポチは 60 m はなれていて、それぞれ毎秒 1 m および 毎秒 9 m で近づくので、60÷(1+9)=6 秒後に出会う。このとき、ヨシオ君とポチは A から 6 m、お父さんは B から 27 m の位置にいて、その間のきょりは 60-(6+27)=27 (m)
次に、お父さんとポチは、それぞれ毎秒 4.5 m および毎秒 9 m で近づくので、27÷(4.5+9)=2 (秒後) に出会う。
結局、はじめから 6+2=8 (秒間) 移動したことになり、ヨシオ君とお父さんは、それぞれ 8 m、36 m 進んでいるので、EF=60-(8+36)=16 (m)
次に、点 G、H の位置を求める。
点 G、H は EF の 3 等分点にとる以外に、点 G を点 F の位置に、点 H を点 E の位置にとる場合が考えられる。ここで、点 G を点 F の位置に、点 H を点 F から 16 m だけ点 B 寄りにとる場合も考えられるが、答えは同じになる。
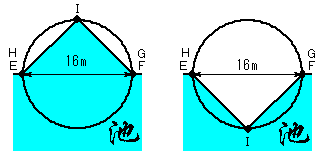
三角形 GHI の面積が最大になるように 3 点 G、H、I をとれば、池の面積が最大および最小となるので、点 G、H を EF の 3 等分点にとるよりも、図のように、点 G を点 F の位置に、点 H を点 E の位置にとるとよい。このとき、三角形 GHI の面積が最大になるのは、点 I を図のような位置 (EI=FI となる位置) にとったときで、その面積は 16×8÷2=64 (m²) である。したがって、池の面積の
(1) 最小値は 3600-64=3536 (m²)
(2) 最大値は (3600+64)÷100=36.64 (a)
06. 999999 個の加算(川田 智之 さん)
次の加算を 999999 項(個)までしなさい。分母は一定の決まりで増加しています。
1/2+1/6+1/12+1/20+1/30+1/42+1/56+1/72+1/90+1/110+…
〔解答・解説〕求める和は
1/(1×2)+1/(2×3)+……+1/(999999×1000000)
=(1/1-1/2)+(1/2-1/3)+……+(1/999999-1/1000000)
=1-1/1000000=999999/1000000=0.999999
07. 逃げろや逃げろ(高橋 道広 さん)
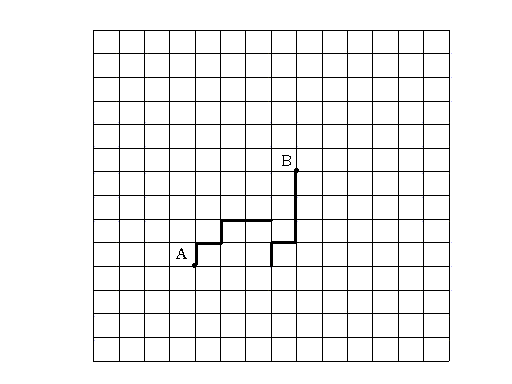
図のように碁盤の目状の道があります。この道の点 A には鬼が、点 B には桃太郎がいます。鬼と桃太郎は、同じ時刻に出発して、同じ速さで、1 分間に 1 ブロック(交差点から、次の交差点まで)ずつ進みます。進む方向を変えるための時間はかかりません。また、鬼は、図の中の道を右または上にしか進めず、桃太郎は左または下にしか進めません。鬼が桃太郎に「見つかる」というのは、「鬼と桃太郎が、同じ時刻に、同じ道の線上にいるとき」とします。たとえば、図の太線の道を鬼と桃太郎が進むとすると、5 分後に、鬼は「見つかって」しまいます。(桃太郎は後ろにも目があるんです)。(^。^)
桃太郎と鬼が同時に出発して、5 分たったとします。まだ鬼は桃太郎に一度も「見つかって」いません。
このとき、鬼と桃太郎の通った道筋の組み合わせは何通りでしょうか。
〔解答・解説〕相対的に考える。
すなわち、桃太郎が動かず、鬼が 1 分間に 2 ブロック移動すると考える。
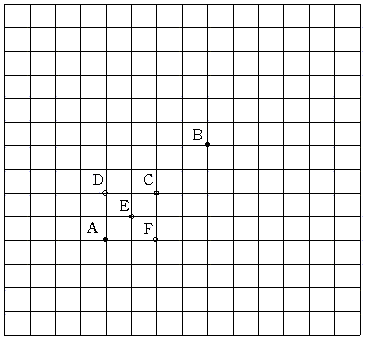
たとえば、上図のように鬼と桃太郎がそれぞれ B、C のような位置関係になったとして、その 1 分前の位置を考える。
(鬼の進み方、桃太郎の進み方) が
(右、左) の場合、鬼は D から移動したことになり、
(右、下)、(上、左) の場合、鬼は E から移動したことになり、
(上、下) の場合、鬼は F から移動したことになる。
すなわち、B、C の位置関係になる場合の数は、(D の場合の数)+(E の場合の数)×2+(F の場合の数) となる。
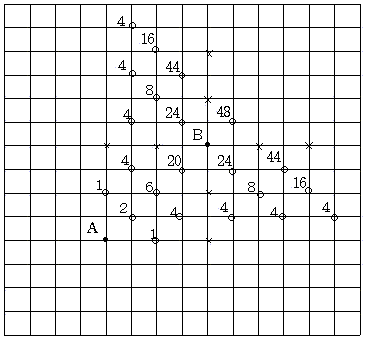
他の位置でも同様のことが成り立つので、下図のように交差点上に次々に場合の数を書き込んでいくと、答えは
(4+16+44)×2+48=176 (通り) となる。
ここで、×印の場所では桃太郎に見つかってしまうので、0 通りとしている。
08. 12 月 1 日 23 時 11 分開始(tm-kimura さん)
今、アキさんと田中さんでゲームを始めました。
ここに、12 本、1 本、23 本、11 本の 4 つのマッチ棒の山があります。ルールは、好きな山から 1 本以上のマッチ棒を交互に取っていき、最後にマッチ棒を取った方が勝ちです。先手番となったアキさんは、6 分ほど考えた後、「私の勝ちですね!」といいながら手を動かしました。
〔問題〕どの山から何本のマッチ棒を取り去ったでしょう?
一度にひとつの山から全てのマッチ棒を取り去る事は構いませんが、二山にまたがってはいけません。また、取り去る山はその都度好きな山を選べます。何人の方がアキさんより早いか楽しみにしてます。
〔解答・解説〕1) 4 つの山がくずれ、2 つの山になったときは、2 つの山の数を同じにして手をわたす。相手が何本かくずしたら、同じ数を取り去り、再び 2 つの山を同じ数にする。そして、最終的には (2,2) にして手をわたせばよい。(1,2) で返されたときは (1,1) にしてわたす。(0,2) で返されたときは 2 本とも取り去れば勝ちとなる。
2) 3 つの山になったときは、(1,2,3) にしてわたせばよい。
- (0,2,3) で返されたときは (0,2,2) にしてわたす。
- (1,1,3) で返されたときは (1,1,0) にしてわたす。
- (1,0,3) で返されたときは (1,0,1) にしてわたす。
- (1,2,2) で返されたときは (0,2,2) にしてわたす。
- (1,2,1) で返されたときは (1,0,1) にしてわたす。
- (1,2,0) で返されたときは (1,1,0) にしてわたす。
また、(1,4,5) にしてわたしてもよい。
- (0,4,5) で返されたときは (0,4,4) にしてわたす。
- (1,3,5) で返されたときは (1,3,2) にしてわたす。
- (1,2,5) で返されたときは (1,2,3) にしてわたす。
- (1,1,5) で返されたときは (1,1,0) にしてわたす。
- (1,0,5) で返されたときは (1,0,1) にしてわたす。
- (1,4,4) で返されたときは (0,4,4) にしてわたす。
- (1,4,3) で返されたときは (1,2,3) にしてわたす。
- (1,4,2) で返されたときは (1,3,2) にしてわたす。
- (1,4,1) で返されたときは (1,0,1) にしてわたす。
- (1,4,0) で返されたときは (1,1,0) にしてわたす。
このように追いつめていくと、(2,4,6) や (3,5,6) の勝ち筋が導き出される。
3) 4 つの山のときは、(1,1,2,2)、(1,2,5,6)、(2,3,4,5) などが勝ち筋である。
(1,1,2,2) にしてわたしたときを考える。
- (0,1,2,2) で返されたときは (0,0,2,2) にしてわたす。
- (1,0,2,2) で返されたときは (0,0,2,2) にしてわたす。
- (1,1,1,2) で返されたときは (1,1,1,1) にしてわたす。
- (1,1,0,2) で返されたときは (1,1,0,0) にしてわたす。
このことから、(X,X,Y,Y) の形が勝ち筋であることが分かる。
(2,3,4,5) にしてわたしたときを考える。
- (1,3,4,5) で返されたときは (1,0,4,5) にしてわたす。
- (0,3,4,5) で返されたときは (0,1,4,5) にしてわたす。
- (2,2,4,5) で返されたときは (2,2,4,4) にしてわたす。
- (2,1,4,5) で返されたときは (0,1,4,5) にしてわたす。
- (2,0,4,5) で返されたときは (1,0,4,5) にしてわたす。
- (2,3,3,5) で返されたときは (2,3,3,2) にしてわたす。
- (2,3,2,5) で返されたときは (2,3,2,3) にしてわたす。
- (2,3,1,5) で返されたときは (2,3,1,0) にしてわたす。
- (2,3,0,5) で返されたときは (2,3,0,1) にしてわたす。
- (2,3,4,4) で返されたときは (2,2,4,4) にしてわたす。
- (2,3,4,3) で返されたときは (2,3,2,3) にしてわたす。
- (2,3,4,2) で返されたときは (2,3,3,2) にしてわたす。
- (2,3,4,1) で返されたときは (2,3,0,1) にしてわたす。
- (2,3,4,0) で返されたときは (2,3,1,0) にしてわたす。
このように、相手が返す手を場合分けし追いつめていくと、大変な作業ではあるが、(1,6,11,12) も勝ち筋の一つであることが見出せる。
一般に、次の解法が知られている。
1)~3) で見てきた勝ち筋を以下のように二進法で表し、それぞれのけたごとに合計すると、どのけたも偶数になっていることが分かる。
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
このように、どのけたの合計も偶数にして相手にわたすと、少なくとも一つのけたは奇数になって返される。そこで、再び適当な山をくずし、すべてのけたを偶数にしてわたせばよい。
この問題における勝ちパターンの例を以下に示す。
⇒は相手にわたすことを、→は自分に返ってくることを意味する。
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
したがって、答えは「23 本の山から 17 本のマッチを取り去った」となる。
09. 割合の問題です(辻。 さん)
3 種類の水道 A、B、C と空の容器が 1 つあります。これらの水道を単独で使用するときは、複数同時に使用する時に比べて単位時間あたりに出る水の量が 15 % 多くなります。
これらの水道のうち 2 種類を同時に使って、この容器を満杯にするまでの時間をはかったところ、水道 A と水道 B では 7 分 30 秒、水道 B と水道 C では 5 分ちょうど、水道 C と水道 A では 3 分 45 秒かかりました。
では、それぞれの水道を単独で A、B、C の順に使った場合、この容器が満杯になるのに何分何秒かかりますか。ただし、容器の 3 分の 1 まで水がたまったら水道 A の蛇口は閉め、同時に水道 B を使用し、容器の 3 分の 2 まで水がたまったら、水道 B の蛇口は閉め、この後満杯になるまで水道 C を使用します。なお、蛇口を閉めてから次の蛇口を開くまでの時間は無視できるものとします。
〔解答・解説〕2 種類同時に使用した場合の水道 A、B、C の 1 分間あたりの水の量を、それぞれ a、b、c とすると、a+b=2/15、b+c=1/5、c+a=4/15 であるから、a=1/10、b=1/30、c=1/6
単独で使用すると水の量は 15 % 増えるから、かかる時間は
1/3÷(1/10×115/100)+1/3÷(1/30×115/100)+1/3÷(1/6×115/100)=40/3 (分)=13 (分) 20 (秒)
10. うろうろしちゃった(老眼鏡 さん)
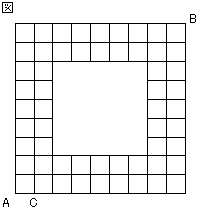
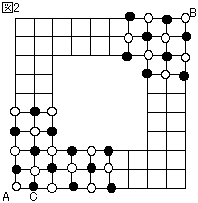
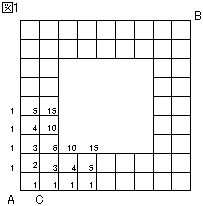
図のように、碁盤の目から真ん中が抜け落ちたような、タテ、ヨコそれぞれ平行な何本かの道路があります。
道路上を、A 点から B 点まで進むことを考えます。
(1) 図の A 点から B 点まで、遠回りしないで行く方法は何通りありますか。
(2) 図の A 点から、まず C 点に進み、その後は自由に進んで、すべての格子点を 1 回ずつ通って B 点まで行く方法は何通りありますか。
注:格子点とは、十字型の点でだけでなく、T 字型および L 字型とその回転した交点の全てを意味しています。
〔解答・解説〕
(1) 図 1 のように、道順の数を次々と書き込んでいくと、2756 通りとなる。
(2) 図 2 のように、すべての格子点に白、黒の碁石を交互に並べると、白、黒とも 42 個ずつで、A、B はともに白となる。
A から B までの道筋をどのように選んでも、石の色は白黒交互に変化して進むことになる。
A、B はともに白であるが、白黒同数の石を「白黒白黒……黒白」と並べることはできないから、答えは 0 通りである。
11. 壱萬円(Nagahiro,Y. さん)
10 円玉、50 円玉、100 円玉、500 円玉を組み合わせて合計 1 万円にするには何通りの方法があるでしょう。ただし、使わない貨幣があってもよいとします。
〔解答・解説〕500 円玉の使用枚数で場合分けをする。
1) 20 枚使用する場合:
他の硬貨は使用できないので 1 通り
2) 19 枚使用する場合:
10000-500×19=500 円を他の 3 種類の硬貨で組み合わせる。
2-a) 100 円玉を 5 枚使用する場合:
他の硬貨は使用できないので 1 通り
2-b) 100 円玉を 4 枚使用する場合:
他の 2 種類の硬貨で 100 円を組み合わせる。
50 円玉の使用枚数は 0、1、2 枚のいずれかであるから 3 通り
2-c) 100 円玉を 3 枚使用する場合:
他の 2 種類の硬貨で 200 円を組み合わせる。
50 円玉の使用枚数は 0~4 枚のいずれかであるから 5 通り
2-d) 100 円玉を 2 枚使用する場合:
他の 2 種類の硬貨で 300 円を組み合わせる。
50 円玉の使用枚数は 0~6 枚のいずれかであるから 7 通り
2-e) 100 円玉を 1 枚使用する場合:
他の 2 種類の硬貨で 400 円を組み合わせる。
50 円玉の使用枚数は 0~8 枚のいずれかであるから 9 通り
2-f) 100円玉を使用しない場合:
他の 2 種類の硬貨で 500 円を組み合わせる。
50 円玉の使用枚数は 0~10 枚のいずれかであるから 11 通り
よって、500 円玉を 19 枚使用する場合の組合せは
1+3+5+7+9+11=36 (通り)
3) 18 枚使用する場合:
10000-500×18=1000 円を他の 3 種類の硬貨で組み合わせる。
3-a) 100 円玉を 10 枚使用する場合:
他の硬貨は使用できないので 1 通り
3-b) 100 円玉を 9 枚使用する場合:
他の 2 種類の硬貨で 100 円を組み合わせる。
50 円玉の使用枚数は 0、1、2 枚のいずれかであるから 3 通り
3-c) 100 円玉を 8 枚使用する場合:
他の 2 種類の硬貨で 200 円を組み合わせる。
50 円玉の使用枚数は 0~4 枚のいずれかであるから 5 通り
3-d) 100 円玉を 7 枚使用する場合:
他の 2 種類の硬貨で 300 円を組み合わせる。
50 円玉の使用枚数は 0~6 枚のいずれかであるから 7 通り
3-e) 100 円玉を 6 枚使用する場合:
他の 2 種類の硬貨で 400 円を組み合わせる。
50 円玉の使用枚数は 0~8 枚のいずれかであるから 9 通り
3-f) 100 円玉を 5 枚使用する場合:
他の 2 種類の硬貨で 500 円を組み合わせる。
50 円玉の使用枚数は 0~10 枚のいずれかであるから 11 通り
3-g) 100 円玉を 4 枚使用する場合:
他の 2 種類の硬貨で 600 円を組み合わせる。
50 円玉の使用枚数は 0~12 枚のいずれかであるから 13 通り
3-h) 100 円玉を 3 枚使用する場合:
他の 2 種類の硬貨で 700 円を組み合わせる。
50 円玉の使用枚数は 0~14 枚のいずれかであるから 15 通り
3-i) 100 円玉を 2 枚使用する場合:
他の 2 種類の硬貨で 800 円を組み合わせる。
50 円玉の使用枚数は 0~16 枚のいずれかであるから 17 通り
3-j) 100 円玉を 1 枚使用する場合:
他の 2 種類の硬貨で 900 円を組み合わせる。
50 円玉の使用枚数は 0~18 枚のいずれかであるから 19 通り
3-k) 100 円玉を使用しない場合:
他の 2 種類の硬貨で 1000 円を組み合わせ。
50 円玉の使用枚数は 0~20 枚のいずれかであるから 21 通り
よって、500 円玉を 18 枚使用する場合の組合せは
1+3+5+7+9+11+13+15+17+19+21=121 (通り)
以上のことから、500 円玉の枚数による場合分けについて、次のことが分かる。
- 500 円玉の使用枚数が 1 枚減るごとに、100 円玉の使用枚数による場合分けが 5 通り増える。
- 100 円玉の使用枚数が 1 枚減るごとに、50 円玉の使用枚数の最大値は 2 枚増える。
- 500 円玉と 100 円玉の使用枚数による場合分けを行なったとき、各場合の組合せの数は 50円玉の使用可能枚数の最大値に 1 を加えたものになる。(例えば、500 円玉 10 枚、100 円玉 20 枚の場合、10000-500×10-100×20=3000 (円) を他の 2 種類の硬貨で組み合わせる。50 円玉の使用枚数は 0~60 枚のいずれかであるから 61 通り。)
したがって、500 円玉の使用枚数の場合分けによる組合せは以下のようになる。
1) 20 枚使用する場合:1 通り
2) 19 枚使用する場合:1+3+5+7+9+11=36 (通り)
3) 18 枚使用する場合:1+3+5+…+19+21=121 (通り)
4) 17 枚使用する場合:1+3+5+…+29+31=256 (通り)
5) 16 枚使用する場合:1+3+5+…+39+41=441 (通り)
6) 15 枚使用する場合:1+3+5+…+49+51=676 (通り)
7) 14 枚使用する場合:1+3+5+…+59+61=961 (通り)
8) 13 枚使用する場合:1+3+5+…+69+71=1296 (通り)
9) 12 枚使用する場合:1+3+5+…+79+81=1681 (通り)
10) 11 枚使用する場合:1+3+5+…+89+91=2116 (通り)
11) 10 枚使用する場合:1+3+5+…+99+101=2601 (通り)
12) 9 枚使用する場合:1+3+5+…+109+111=3136 (通り)
13) 8 枚使用する場合:1+3+5+…+119+121=3721 (通り)
14) 7 枚使用する場合:1+3+5+…+129+131=4356 (通り)
15) 6 枚使用する場合:1+3+5+…+139+141=5041 (通り)
16) 5 枚使用する場合:1+3+5+…+149+151=5776 (通り)
17) 4 枚使用する場合:1+3+5+…+159+161=6561 (通り)
18) 3 枚使用する場合:1+3+5+…+169+171=7396 (通り)
19) 2 枚使用する場合:1+3+5+…+179+181=8281 (通り)
20) 1 枚使用する場合:1+3+5+…+189+191=9216 (通り)
21) 使用しない場合:1+3+5+…+199+201=10201 (通り)
1)~21) を合計して、73871 通り。
12. サラのママはたいへんなのだ 2(サラのママ さん)
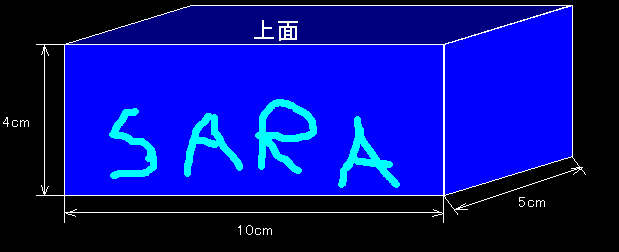
サラのママは毎朝、サラのお弁当におにぎりを作ります。でも、サラは、円柱で同じ体積(合同であること)のおにぎりでないと食べてくれません。お弁当の容積は限られていますが、サラのママは、サラにできるだけたくさん食べてもらいたくて、円柱のおにぎりをできるだけ詰めています。ただ、ノリ同士がくっついてしまうのがいやなので、おにぎりのまわりには 1 個ずつ紙で仕切りをつけることにします。
たて 5 cm、横 10 cm、高さ 4 cm のお弁当箱の容積に、合同な円柱の形をした仕切りつきのおにぎりをできるだけたくさん詰めるとき、お弁当の中のおにぎりの総体積は何 cm³ になるでしょう?ただし、
- サラのママの手の精度はよくありません。直径において、cm 単位のおにぎりまで作れますが、直径でミリ単位のおにぎりは作れません。
例:円柱の直径 2.5 cm のおにぎりは不可能。直径 2 cm か直径 3 cm なら作れます。 - サラはうまくお箸が使えないため、おにぎりは、寝ていないとつかめません。お弁当のふたを開けたとき、おにぎりの底面が見えないようにおにぎりを詰めたいのです。全ての円柱の中心軸は互いに平行で、お弁当箱のどれかの 1 つの面と垂直になるようにします。
- おにぎりは円柱を 1 つのかたまりとしてお弁当箱にいれるのであって、おにぎりを切って円柱でなくなった形を分割して詰めることはできません。
- おにぎりには四角柱の形になるように仕切りをつけるものとします。四角柱の底面は正方形でその 1 辺の長さはおにぎりの底面の円の直径と同じ長さとし、四角柱の高さはおにぎりの高さと同じとします。隣のおにぎりと接しているかどうかにかかわらず、必ず仕切りはつけますが、仕切りじたいには厚みがないもの、としてください。
〔解答・解説〕
1) 円柱の高さを 4 cm とする場合:
1-a) 直径 5 cm、高さ 4 cm の円柱 2 個、すなわち 5/2×5/2×3.14×4×2=157 (cm³)
1-b) 直径 1 cm、高さ 4 cm の円柱 50 個、すなわち 1/2×1/2×3.14×4×50=157 (cm³)
2) 円柱の高さを 5 cm とする場合:
2-a) 直径 2 cm、高さ 5 cm の円柱 10 個、すなわち 2/2×2/2×3.14×5×10=157 (cm³)
2-b) 直径 1 cm、高さ 5 cm の円柱 40 個、すなわち 1/2×1/2×3.14×5×40=157 (cm³)
3) 円柱の高さを 10 cm とする場合:
直径 1 cm、高さ 10 cm の円柱 20 個、すなわち 1/2×1/2×3.14×10×20=157 (cm³)
いずれの場合も、おにぎりの総体積は 157 (cm³)
13. 大蛇♪大蛇♪ 大蛇♪大蛇♪ 大蛇八兄弟♪(Taro さん)
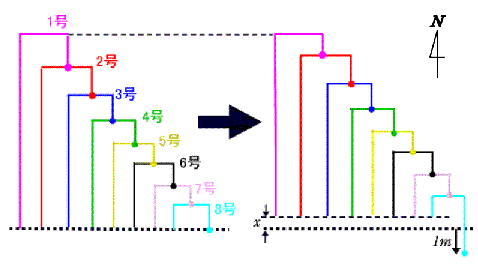
珍種の巨大な蛇(へび)がいます。この蛇が静止している時には以下のような特徴があります。
- 頭は南の方角に向けます。また、頭から尾に向かう適当な 2 点で体を反時計回りに直角に曲げます。曲げた区間を頭の方から順に「頭」、「胴」、「尾」と呼びます。「胴」の長さは常に 2 m です(蛇が体を曲げる箇所は動く際に自由に変えられます)。
- この蛇が同じ仲間の「胴」を噛むときは、「頭」の先にある口で、「胴」の真ん中の点を噛みます。
この蛇の 8 兄弟がいます。長男から順に 1 号、2 号、……、8 号と名づけられています。現在、1 号が 2 号の、2 号が 3 号の、……、7 号が 8 号の胴を噛んでいます。また、全ての蛇の尾の先と 8 号の頭の先が、左図のように西から東へ一直線に並んでいました。
いま 1 号から 7 号が口を開けた際に、8 号が頭より南 1 m にある蛙を食べるために頭をそこへ動かしました。それにつられて 1 号から 7 号が体を動かし先ほど噛んでいた蛇の胴を噛んで静止しました(噛んだ場所は異なります)。そのとき 1 号の胴は動く前と全く同じ場所にあり、また全ての蛇の尾の先は西から東へ右図のように一直線に並んでいます。
それでは蛇 1 号の尾は何 cm 北に動いたでしょうか(図の x の長さです)。
〔解答・解説〕2 号の頭と尾、および 1 号の胴を固定し、1 号の尾を動かしてみる。
1 号の尾が x cm 北に動くと、1 号の頭は x cm 南に動く。その結果、2 号の胴 (=1 号の頭) は x cm 南に動く。このままでは、2 号の尾と頭がそれぞれ x cm 短くなってしまうので、その分の x×2 cm と、2 号の尾の実際の移動距離 x cm の合わせて x×3 cm だけ 2 号の頭は南に動くことになる。
同様にして、3 号の頭は x×(3×2+1)=x×7 (cm) 南に動く。
さらに、4 号の頭は x×(7×2+1)=x×15 (cm) 南に動く。
これを繰り返していくと、8 号の頭は x×255 cm 南に動くことになる。
x×255=100 であるから、x=20/51 (cm)。
14. さんかく(Y氏 さん)
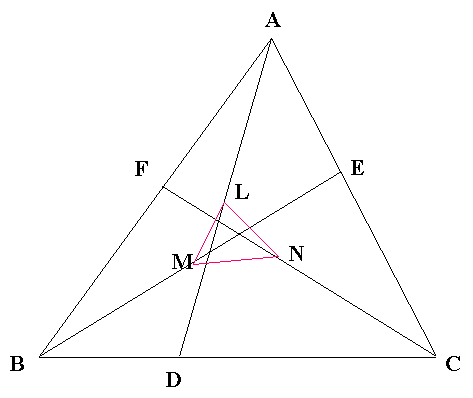
三角形 ABC があります。辺 AB の中点を F、辺 BC 上に点 D をとり BD:DC=1:2、辺 CA 上に点 E をとり CE:EA=4:3 とします。さらに AD、BE、CF の中点をそれぞれ L、M、N とします。
三角形 ABC の面積が 17 cm² のとき三角形 LMN の面積は何 cm² ですか。
〔解答・解説〕BC、CA の中点をそれぞれ Q、R とする。
中点連結定理より、MQ=EC/2、MF=EA/2 かつ MQ//EC、MF//EA であるから、F、M、Q は一直線上にあり、MQ:MF=EC:EA=4:3
同様に、QN:NR=BF:FA=1:1、RL:LF=CD:DB=2:1
よって、
(三角形 FML)÷(三角形 FQR)=3/7×1/3=1/7
(三角形 MQN)÷(三角形 FQR)=4/7×1/2=2/7
(三角形 LNR)÷(三角形 FQR)=1/2×2/3=1/3
であり、(三角形 LMN)÷(三角形 FQR)=1-(1/7+2/7+1/3)=5/21
したがって、(三角形 LMN)=(三角形 FQR)×5/21=(三角形 ABC)÷4×5/21=17÷4×5/21=85/84 (cm²)
15. 青春の光と影(中学への算数にチャレンジ さん)
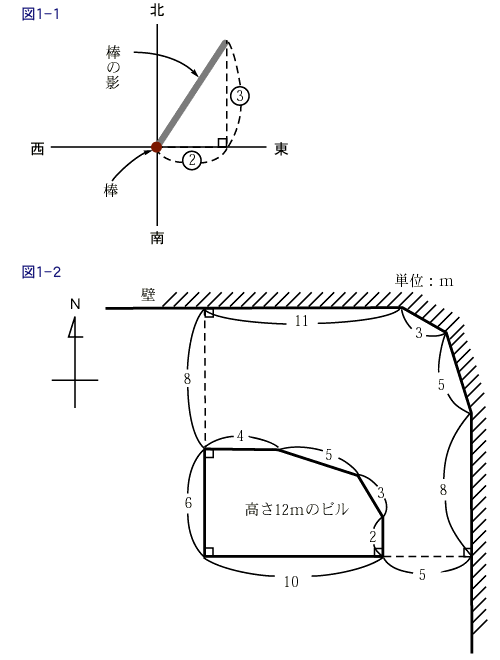
図のように、六角形の底面を持ち高さ 12 m である柱状のビルと、ビルの高さより高い壁があります。
いま、このビルの太陽光線によってできる影を考えます。1 年のうちで、A(○月○日○時○分)のときには、ビルの影が、250 m² になり、B(△月△日△時△分)のときには、239 m² になります。A のときと B のときとでは、地面にできたビルの影は合同な図形になり、地面に鉛直に立てた棒の影も同方角の、東方向、北方向に 2:3(2:3 の方角)にできます。
このとき、A のときと、B のときの、棒によってできる影の長さの比を求めなさい。ただし、ビルの影の面積とは、地面にできた影と壁にできた影の両方の面積を足したもので、ビルの底面、側面は含みません。
〔解答・解説〕A、B いずれの場合も地面にできた影は図 1 のようになり、その面積は
14×15-6×10-16/3×8÷2-5×15/2÷2=1319/12 (m²)
壁にできる影の面積は
A のとき、250-1319/12=1681/12 (m²)
B のとき、239-1319/12=1549/12 (m²)
水平に光が当たったとき壁にできる影の面積は (17/3+3+5+1/2)×12=170 (m²)
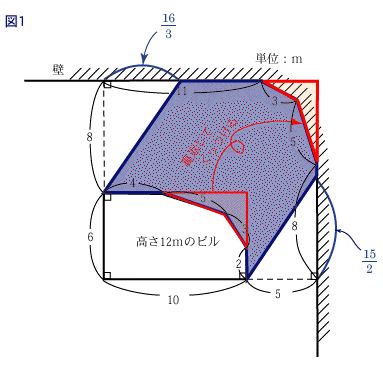
ビル上面で、長さ 4 m、5 m、3 m、2 m のいずれかの辺上の点を通る 2:3 方向の断面は図 2 のようになる。水平方向と太陽光線のなす角は A のとき α で、B のとき β である。
ここで、水平から光が当たったときには影になるが、A のときと B のときには影にならない部分に着目する。どの点を通る断面図であっても α、β の値は等しいので、A のときと B のとき影にならない部分の長さの比は一定である。
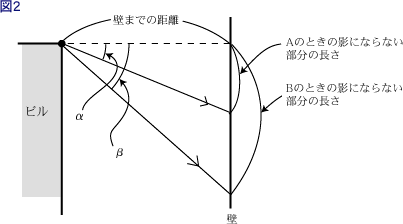
よって、図 3 において、a:b=c:d であり、B のとき影にならない部分は、A のとき影にならない部分を直線 l に関して、たてに何倍かした図形になっている。すなわち、(A のとき影にならない部分の長さ):(B のとき影にならない部分の長さ)=(A のとき影にならない部分の面積):(B のとき影にならない部分の面積) となる。
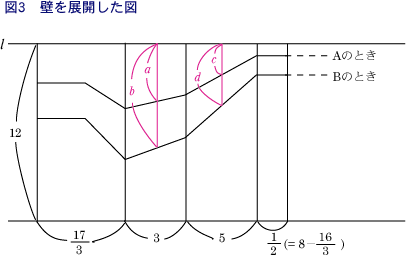
図 4 において、三角形 CDE と 三角形 CFG が相似であることと、CF:CD=(B のときの影の長さ):(A のときの影の長さ) であることにより、(B のときの影の長さ):(A のときの影の長さ)=(A のとき影にならない部分の面積):(B のとき影にならない部分の面積) である。
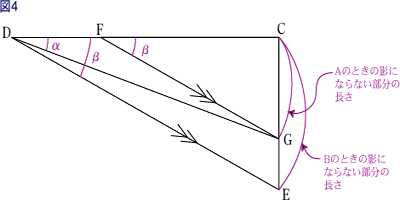
したがって、A のときと B のときの、棒によってできる影の長さの比は、水平に光が当たったとき壁にできる影において、影にならない部分の面積の逆比であるから、
(170-1549/12):(170-1681/12)=491:359
16. がんばれ F 君 Part 2(BossF さん)
F 君は、夏期講習で隣の子が持ってたスピログラフ(注 1)に感動し、お母さんに、ねだりました。すると返ってきた返事は、
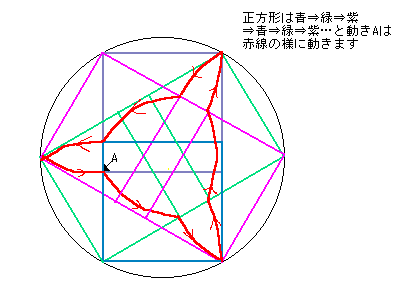
「なに考えてるんでしょうね、この子は。5 年生でしょ、もうすぐ受験よ。でも、この問題が解けたら、考えても良いわ……。半径 4 cm の円の内部で、1 辺 4 cm の正方形を円周に沿って滑らないように回転させていったとき、1 つの頂点はある図形を、描くの。その図形の面積を求めてみて。」
さっそく、F 君、図を描いてみました。するとムーミン谷の誰かさんに似た、綺麗な図が……。「さすが、かあさん」と思いながら、解き始めましたが、どうしても解けません。
そこで、お母さんに質問にいったところ、
「あら、しまったわ、確かに小学校の範囲じゃ無理ね。」
といって、
「ひとよひとよに……えっと、によよくよく……だったかしら?」
となにやら呪文を唱えながら、図をかいてくれて、それを参考にやるようにといわれました。
さて、翌日「ふ~、やっとできたよ~!」と F 君がお母さんのとこに持っていったら、
「あら、昨日のやったの?ごめんね~。お母さん、あなたが学校行ってるあいだに、いろいろ探してみたんだけど、スピログラフ、もう、売ってないみたいよ。」
といわれてがっくり……。
さて問題です。半径 4 cm の円の内部で、1 辺 4 cm の正方形を円周に沿って滑らないように回転させていった時(注 2)、1 つの頂点が、元の位置に戻ってくるまでに描く曲線によって囲まれる図形の面積は何 cm² ですか。四捨五入して小数第 1 位まで求めてください。必要ならば、F 君のお母さんの図を使ってください。なお、解き方によってどうしても割り切れない割り算などが現れた場合は、答えに影響しないよう十分な桁数をとりながら計算を進めてください。
注 1:御存知ない方は(御存知の方も) http://www.zusaku.com/2kspiro.html をご覧になってください。
注 2:右図のように動かします。
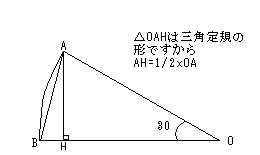
〔解答・解説〕正方形は 1 回につき 30° 回転するから、曲線は中心角 30° の扇形の弧を描き、その半径は 4 cm または 1 辺 4 cm の正方形の対角線の長さである。
まず、扇形の弧と弦に囲まれた部分の面積を考える。
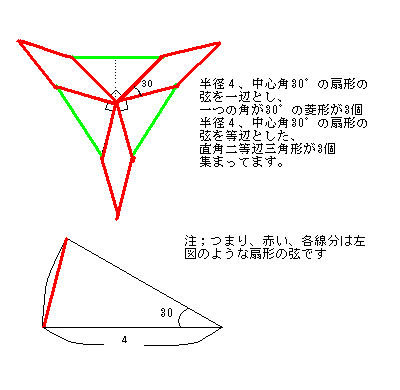
半径が 4 cm の場合 (右図)、4×4×3.14×1/12-4×2÷2 で、これが 6 個あるから、全部で (3.14×4/3-4)×6=25.12-24=1.12 (cm²)…①
半径が 1 辺 4 cm の正方形の対角線の長さの場合 (下図)、(4×4×3.14×1/12-4×2÷2)×2 で、これが 3 個あるから、全部で (3.14×4/3-4)×2×3=25.12-24=1.12 (cm²)…②
次に、弦で囲まれた部分の面積を考える (下図)。
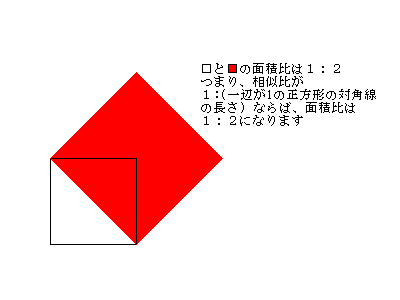
ひし形を、頂角 30°の二等辺三角形 2 つと考えれば、お母さんの図と①の考え方から、2.07×(2.07×1/2)÷2×2 で、これが 3 個あるから 2.07×2.07×1/2×3…③
直角二等辺三角形は 2.07×2.07÷2 で、これが 3 個あるから 2.07×2.07×1/2×3…④
③、④をあわせて、2.07×2.07×3=12.8547 (cm²)…⑤
①、②、⑤より、求める面積は 1.12+1.12+12.8547=15.0947≒15.1 (cm²)
17. かながわの景勝 50 選(田村 稔 さん)
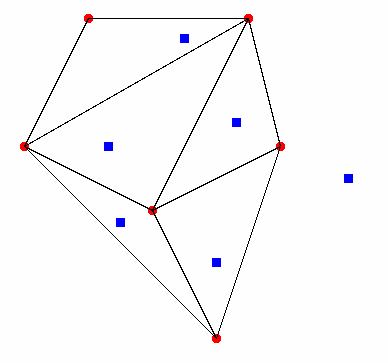
神奈川県には、観光協会が 1979 年に制定した「かながわの景勝 50 選」で選ばれた風光明媚な場所が 50 ヶ所あります。そこには「かながわの景勝 50 選」であることを示す石碑が立っています。みのるさんは、その石碑全部と写真を撮ることに挑戦中です。
ある日、みのるさんは地図上で、まだ行っていない場所(赤点)どうしを、辺が交わらないように結んで、できるだけ多くの三角形を作りました。すると、すべての三角形に 1 つずつすでに行った場所(青点)が入り、さらにできた図形の外側にも 1 つだけ行った場所(青点)がありました。(図は行った場所が 6 ヶ所、行ってない場所が 6 ヶ所の場合の例です)
みのるさんがすでに行った場所は最大何ヶ所でしょうか?
注:この問題での景勝の場所は実際の場所とは関係ありません。景勝の配置によっては行った場所の数は異なりますが、その中で最大の数を解答してください。
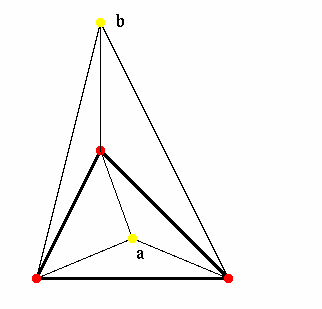
〔解答・解説〕三角形を一つ作るには、頂点が 3 個必要である。ここに頂点を一つ追加して、できるだけ三角形の数を増やすには、三角形の内部 (a) または外部から 3 頂点に線が結べる位置 (b) に頂点を追加すればよい。このとき、どちらの場合も三角形が 2 個増える。その結果、外周は三角形になり、その内部は三角形で仕切られる (右図)。
外周が n 角形 (n>3) の場合、頂点を外部に一つ追加すると、三角形は最大で (n-1) 個増える。また、n 角形は簡単な変形を繰り返すことにより、外周を三角形にすることができる。このとき、三角形は (n-3) 個増える (下図)。
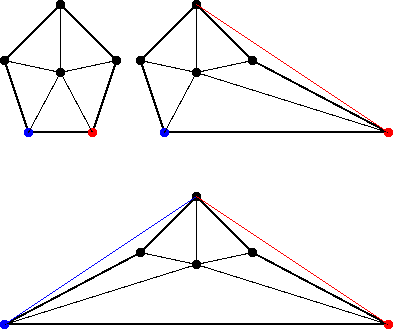
よって、ある頂点数において、外周が三角形の場合の三角形の最大数を x とすると、外周が n 角形の場合の三角形の最大数は x-(n-3) である。ここに頂点を一つ追加すると、三角形は最大で (n-1) 個増え、三角形の最大数は x-(n-3)+(n-1)=x+2 となる。
また、外周が三角形の場合は頂点を一つ追加すると、三角形は最大で 2 個増え、三角形の最大数は x+2 となる。したがって、外周が三角形の場合を考えれば十分である。
頂点を一つ増やすごとに、三角形の最大数は 2 ずつ増えるので、頂点の数と三角形の最大数の関係は次のようになる。
| 頂点 | 3 | 4 | 5 | …… | 17 | 18 | 19 | …… |
| 三角形 | 1 | 3 | 5 | …… | 29 | 31 | 33 | …… |
題意より、頂点の数と三角形の最大数の和が 49 であればよい。上表から、そのときの頂点の数は 18 であり、これはまだ行ってない場所の数である。
したがって、すでに行った場所は 50-18=32 (ヶ所) となる。
18. 算数で解いてくださいね。(ぶぶおパパ さん)
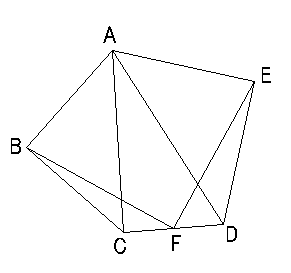
図のように、面積が 100 cm² の五角形 ABCDE があります。F は辺 CD の真ん中の点で、AB=BC、DE=EA、BF=FE です。また、∠ABC、∠DEA、∠BFE はいずれも直角です。
さて、BF の長さは何 cm でしょうか?
〔解答・解説〕図のように、2 つの三角形を移動すると正方形ができる。
100=10×10 より、BF=10 (cm)
19. カラアゲテイショク(かぶとっ さん)
ある大阪府の有名進学校で模試が行われ本日 12 月 1 日成績が発表されました。その高校に通う三つ子の兄弟 A 君、B 君、C 君が家で親に見せこんな話をしてました。(A、B、C はそれぞれ自分の点数以外知りません)
母 「A と B の点差はちょうど 130 点よ」
B 「うーん、それだけじゃあ A の点数はわからないなぁ」
A 「僕もわからないよ」(※1)
父 「お、A と C の点差は 100 点ぴったりだな」
C 「うーん、わからないなぁ」(※2)
父 「よーし、一番初めにみんなの点数がわかったやつにチェさんの唐揚げ定食を食べさしてやろう。一生懸命考えてみなさい」
A、B、C 「うーん、」(※3)
A 「まだ誰もわかってないのか、じゃあわかった」(※4)
C 「じゃあ、僕もわかった」(※5)
B 「僕もわかったけど、こんなゲーム不公平だよ」
(チェさんの唐揚げ定食はすごく美味しい)
以上のようなことが起こりうる A、B、C の点数の組合わせのうち A + B + C が最大となるような A、B、C の組合わせを求めなさい。ただしこのテストは 1000 点満点とする。また A、B、C はとても頭がいいとします。
※1:A は B の点数がわかっていないものとします。
※2:C は A の点数も B の点数もわかっていないものとします。
※3:3 人とも、他の 2 人の得点のうち少なくとも一方はわかっていないものとします。
※4:A は B の点数も C の点数もわかったものとします。
※5:C は A の点数も B の点数もわかったものとします。
〔解答・解説〕
母 「A と B の点差はちょうど 130 点よ」
B 「うーん、それだけじゃあ A の点数はわからないなぁ」…①
A 「僕もわからないよ」…②
父 「お、A と C の点差は 100 点ぴったりだな」
C 「うーん、わからないなぁ」…③
父 「よーし、一番初めにみんなの点数がわかったやつに、チェさんの唐揚げ定食を食べさしてやろう。一生懸命考えてみなさい」
A、B、C 「うーん」…④
A 「まだ誰もわかってないのか。じゃあわかった」…⑤
C 「じゃあ、僕もわかった」
①の時点で B の点数は 130~870、②の時点で A の点数は 260~740、③の時点で C の点数は 360~640 とわかる。
(A,B,C)=(740,610,640) が題意を満たすことを示す。
- A の立場で考えてみる。
③の時点で C は 640 点とわかる。
④の時点で B の 点数は 610 または 870 とわかっている。もし B が 870 点ならば、②の時点で B は A の点数 (740 点) がわかり、③の時点で B は C の点数 (640 点) がわかる。
よって、B が④のように悩むのはおかしいことになる。
したがって、B は 610 点とわかる。 - C の立場で考えてみる。
③の時点で A の点数は 540 または 740 とわかっている。もし A が 540 点ならば、③の時点で A は C の点数が 440 または 640 とわかる。しかし、C がいずれの点数であっても、③のように C は A の点数を定められないので、④の時点でも A は C の点数がわからない。
よって、A が⑤のように発言するのはおかしいことになる。
したがって、A は 740 点とわかる。
A の点数がわかれば、A と同様の考えで B の点数 (610 点) がわかる。
よって、(A,B,C)=(740,610,640) は題意を満たすことがわかり、このとき、3 人の合計点は 1990 となる。
次に、合計点が 1990 を超える A,B,C の組合せは存在しないことを示す。
C<A<B,C>A<B,C>A>B の 3 つに場合分けして考える。
(A の点数は 260~740 であるから、C<A>B の場合、(A,B,C)=(740,610,640) のとき、3 人の合計点は最大となる。)
- C<A<B の場合:
合計点が 1990 より大きくなるためには (A,B,C)=(654,784,554) 以上が必要である。このとき、B の立場で考えると、②の時点で A の点数がわかり、③の時点で C の点数がわかる。よって、④のように悩むのはおかしい。 - C>A<B の場合:
合計点が 1990 より大きくなるためには (A,B,C)=(587,717,687) 以上が必要であるが、これは③の時点でわかる C の範囲に矛盾する。 - C>A>B の場合:
合計点が 1990 より大きくなるためには (A,B,C)=(674,544,774) 以上が必要であるが、これは③の時点でわかる C の範囲に矛盾する。
したがって、(A,B,C)=(740,610,640) のとき、3 人の合計点 A+B+C は最大値 1990 をとる。
20. 試行錯誤の数え上げ ~実話より~(sugitakukun さん)
『ついにやってきました 2001 年の算数トライアスロン。初挑戦ですがどーぞよろしく。初めて開催を知ったのが 8 月 29 日だからそれからおよそ 90 日。その間に私は 17 歳になりました。まあ苦労して作った問題ですから、4、5 分で解いたりしないよーに。では問題。この文章(=『 』内)には、1 が ( a ) 個、2 が ( b ) 個、3 が ( c ) 個、4が ( d ) 個、5 が ( e ) 個、6 が ( f ) 個、7 が ( g ) 個、8 が ( h ) 個、9 が ( i ) 個、そして、0 が ( j ) 個あります。このときこれらのアルファベットにあてはまる数の組み合わせを全て答えなさい。』
注意:
- ( a )~( j ) に入る数は全て 1 桁です。
- あてはめた数もカウントして文章が成立しなければいけません。……よくわからない人は下の例題を見てください。
- この注意書きや例題に出てくる数はカウントしません。
- 問題になっているのは文章中の数字の数です。例えば、2001 は、「2」、「0」、「0」、「1」、という 4 つの数字に分けて考えます。
例題:「この文には、1 が ( a ) 個、2 が ( b ) 個、3 が ( c ) 個、4 が ( d ) 個あります。」
この例題では、a に 3、b に 1、c に 3、d に 1 というのが答えの 1 つです。なぜなら、これらの数を文にあてはめた時、文に出てくる数は「1、3、2、1、3、3、4、1」となり、「1 が 3 個、2 が 1 個、3 が 3 個、4 が 1 個」になっているからです。ちなみに、a に 2、b に 3、c に 2、d に 1 というのも答えです。確認してみてください。
〔解答・解説〕(a)~(j) 以外に現れる数字の個数は次のようになる。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 個数 | 3 | 3 | 1 | 2 | 2 | 1 | 2 | 2 | 3 | 4 |
(a)~(j) は 1 けたの数であるから、1~9 のいずれか。すなわち、(a)~(j) に 0 は入らないから、0 は 4 個と定まる。よって、4 は 3 個以上となる。
9 の個数について考える。
(a)~(j) に入る数の和は、文章中に出てくる数の個数と同じである。(a)~(j) には 1 個ずつ合計 10 個の数字が入るから、その和は 33 である。
9 が 5 個とすると、(a)~(h) のうち 2 つに 9 が入ることになるが、このとき (a)~(j) の和は最小でも 9+9+1+2+2+1+2+2+5+4=37 となり不適。
9 が 4 個とすると、(a)~(h) のうち 1 つに 9 が入ることになるが、
- 3 が 9 個とすると、(a)~(j) のうち 8 つに 3 が入ることになり、(a)~(j) の和が最小でも 33 を超えてしまうので不適。
- 同様にして、4~8 のいずれも 9 個とはできない
- 1 が 9 個とすると、(a)~(j) のうち 6 つに 1 が入ることになるが、(a)~(j) のうち、たかだか 2 つしか 1 は入らないので不適。
- 同様にして、2 が 9 個とはできない。
よって、9 は 3 個と定まる。
ここで、(a)~(h) 以外に現れる数字の個数は次のようになっている。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 個数 | 3 | 3 | 2 | 3 | 2 | 1 | 2 | 2 |
このとき、(a)~(h) の和は 33-4 (0 の個数) -3 (9 の個数) =26 である。
8 の個数について考える。
8 が 4 個以上とすると、(a)~(h) の和は最小でも 8+8+2+3+2+1+2+4=30 となり不適。
8 が 3 個とすると、(a)~(g) のうち 1 つに 8 が入ることになるが、
- 3~5、7 のいずれかが 8 個とすると、(a)~(h) の和が 26 を超えてしまうので不適。
- 1、2、6 はもはや 8 個にはならないので不適。
よって、8 は 2 個と定まる。
まとめると、次のようになる。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 個数 | 3 | 4 | 2 | 3 | 2 | 1 | 2 |
このとき、(a)~(g) の和は 26-2 (8 の個数) =24 である。
7 の個数について考える。
7 が 4 個以上とすると、(a)~(g) の和は最小でも 7+7+2+3+2+1+4=25 となり不適。
7 が 3 個とすると、(a)~(f) のうち 1 つに 7 が入ることになるが、
- 3~5 のいずれかが 7 個とすると、(a)~(g) の和が 24 を超えてしまうので不適。
- 1、6 はもはや 7 個にはならないので不適。
- 2 を 7 個とすると、3、5、6 は 2 個になるが、もはや 1 も 4 も 6 個にはならない。
よって、7 は 2 個と定まる。
ふたたびまとめると、次のようになる。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 |
| 個数 | 3 | 5 | 2 | 3 | 2 | 1 |
このとき、(a)~(f) の和は 24-2 (7 の個数) =22 である。
1 の個数で場合分けする。1 は 3 個または 4 個である。
1) 1 が 3 個のとき:
6 は 1 個ではない、すなわち 2 個以上になる。6 を 3 個とすると、(a)~(f) の和を 22 にするためには、2、4 が 6 個となるが、3、5 の個数を増やさないといけないので不適。よって、6 は 2 個と定まり、2~5 のいずれかが 6 個である。
まとめると、次のようになる。
| 数字 | 2 | 3 | 4 | 5 |
| 個数 | 6 | 3 | 3 | 2 |
このとき、(b)~(e) の和は 22-3 (1 の個数) -2 (6 の個数) =17 である。
2 を 7 個以上とすると、3~5 のいずれかが 6 個になり、(b)~(e) の和が 17 を超えてしまうので不適。よって、2 は 6 個と定まる。
残る (c)~(e) は 3~5 のいずれかである。
その和は 17-6 (2 の個数) =11 であるが、5 を 4 個以上とすると、(c)~(e) の和が 11 を超えてしまうので不適。
よって、5 は 3 個と定まり、3 は 5 個、4 は 3 個に決まる。
したがって、答えは (a) から順に、(3,6,5,3,3,2,2,2,3,4) となる。
2) 1 が 4 個のとき:
6 は 1 個と定まり、2 は 5 個に決まる。
まとめると、次のようになる。
| 数字 | 3 | 4 | 5 |
| 個数 | 2 | 4 | 3 |
このとき、(c)~(e) の和は 22-4 (1 の個数) -1 (6 の個数) -5 (2 の個数) =12 である。
(c)~(e) は 3~5 のいずれかであるが、3 は 4 個以上にできないから、3 は 3 個と定まり、4 は 5 個、5 は 4 個に決まる。
したがって、答えは (a) から順に、(4,5,3,5,4,1,2,2,3,4) となる。
1)、2) より、答えは (a) から順に、(3,6,5,3,3,2,2,2,3,4)、(4,5,3,5,4,1,2,2,3,4) の 2 通り。
21. Hey Men Zoo K?!(CRYING DOLPHIN さん)
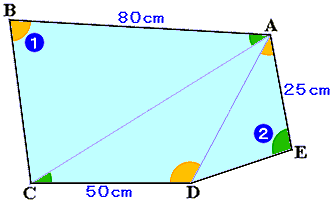
図の五角形 ABCDE の面積は何 cm² と考えられますか?この五角形については、次のようなことがわかっています。
- AB=80 cm、CD=50 cm、EA=25 cm
- 五角形の内角はすべて 180 度より小さい
- ∠ABC+∠ADC+∠DAE=180 度、∠BAC+∠ACD+∠AED=180 度
- ∠ADC>90 度、∠AED>90 度
- ∠AED の大きさは ∠ABC の大きさの 2 倍
〔解答・解説〕図 1 のように、三角形 ABC と三角形 ADE をそれぞれひっくり返す。このとき、∠BCA+∠CAD+∠ADE=540-180×2=180 度であるから、ひっくり返した後の 2 つの辺 BC、DE は一直線になる。ここにできた四角形を PQRS とする (図 2)。
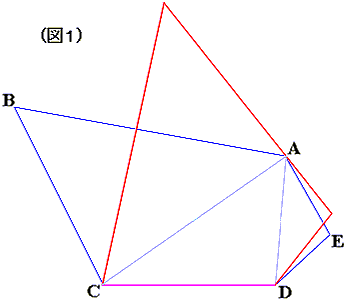
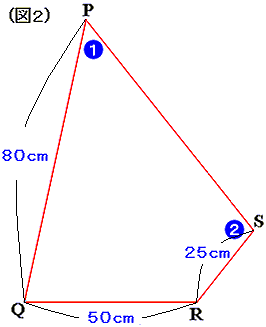
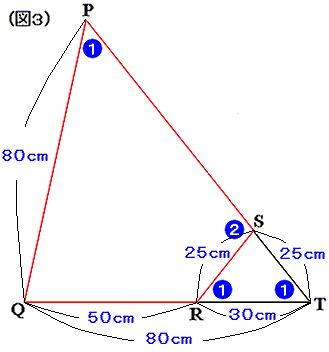
図 2 において、∠P=∠ABC、∠R=∠ADC+∠DAE より、∠P+∠R=180 度である。また、∠S=∠AED>90 度、∠R=∠ADC+∠DAE>∠ADC>90 度である。よって、PS と QR の延長線は図において点 R の右側で交わり、その点を T とする (図 3)。
図 3 において、∠PSR(=∠SPQ×2)=∠SRT+∠STR…①
∠SPQ+∠QRS=180 度であるから、∠SPQ=∠SRT…②
①、②より、∠STR=∠PSR-∠SRT=∠SPQ
よって、三角形 QTP は ∠QTP=∠TPQ の二等辺三角形、三角形 SRT は ∠SRT=∠RTS の二等辺三角形である。しかも、三角形 QPT と三角形 SRTは 2 角が等しいので相似である。その相似比は QP:SR=80:25=16:5 であり、ST=SR=25 cm、QT=PQ=80 cm より、RT=80-50=30 (cm) である。
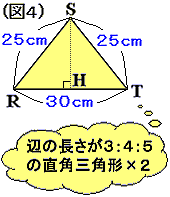
ここからは 三角形 SRT に注目する (図 4)。
S から辺 RT に下ろした垂線の足を H とすると、RH=30÷2=15 (cm)
よって、三角形 SRH は「辺の長さが 3:4:5 の直角三角形」となっているので、SH=25×4/5=20 (cm)
したがって、三角形 SRT の面積は 30×20÷2=300 (cm²)
四角形 PQRS は、三角形 QPT から 三角形 SRT を取り除いたものである。
相似な図形は相似比が a:b のとき、その面積比は (a×a):(b×b) であるから、求める面積は
300×(16×16-5×5)/(5×5)=2772 (cm²)
〔出題者からのコメント〕当初は全然違うアイデアを必要とする問題を考えていたのですが、そのアイデアをひねっているときにふと「図形をひっくり返す」というアイデアが浮かんで、試行錯誤を繰り返した末完成したのがこの問題です。ちょっと条件が多いのが不満なところですが、とある別のアイデアでも簡単に解かれてしまうのを封じる為にはこの方法しか思いつきませんでした。
22. 今年は、数えあげ(ノースダウン さん)
この紙から下の 2 条件を守って切断し、1 片の紙片を切り取ります。ただし、点のみで接するような 2 つ以上の図形は 1 片と見なしません。また、切り取る紙片はへこみのある図形も考えるものとします。
- 切り取った紙片の頂点は a~i のいずれかの点とする。
- 線分で切断する。
反転・回転・移動して重なる場合も、各々 1 通りとして数える場合、紙片の面積が 1 cm² となる切り取り方は( ア )通りで、面積が 3 cm² となる切り取り方は( イ )通りになる。
〔解答・解説〕切り取った紙片は、面積が 0.5 cm² の 2 種類の三角形 (右図) を組み合わせた形である。
まず、面積が 1 cm² となるためには、三角形を 2 個組み合わせればよい。頂点が a~i に一致するように等しい長さの辺どうしを組み合わせて考えると、
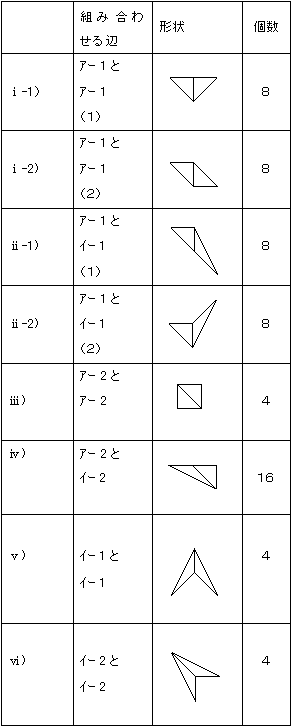
- ア-1 と ア-1 … 2 種類
- ア-1 と イ-1 … 2 種類
- ア-2 と ア-2 … 1 種類
- ア-2 と イ-2 … 1 種類
- イ-1 と イ-1 … 1 種類
- イ-2 と イ-2 … 1 種類
の 8 種類の形をつくることができる。
(イ-3 と イ-3 を組み合わせた場合、ア-1 と ア-1 を組み合わせた図形と同じになる)
この 8 種類の形状の、それぞれの切り取り方は次の表のとおり 60 通りである。
次に、面積が 3 cm² となる場合を考える。
正方形 agic の面積は 4 cm² であるので、この正方形から面積が 0.5 cm² の三角形を 2 個切り取ればよい。三角形 2 個の切り取り方は次の 3 パターンある。
- 三角形 1 を 2 個切り取る
- 三角形 1 と 三角形 2 を 1 個ずつ切り取る
- 三角形 2 を 2 個切り取る
それぞれの場合について、切り取る組合せを数える。そこで、正方形 agic を下図のように 4 ヶ所のエリアに分割して考える。
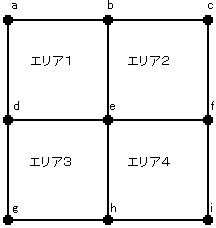
A) 三角形 1 を 2 個切り取る場合:
三角形 1 を条件に合うように切り取ると、エリアをまたいで切り取ることはない。
よって、切り取り方は次の 3 パターンある。
- 1 つのエリアから 2 個切り取る
- 隣り合う 2 つのエリアから 1 個ずつ切り取る
- 対角の 2 つのエリアから 1 個ずつ切り取る
A-1) 1 つのエリアから 2 個切り取る場合:4 通り
A-2) 隣り合う 2 つのエリアから 1 個ずつ切り取る場合:
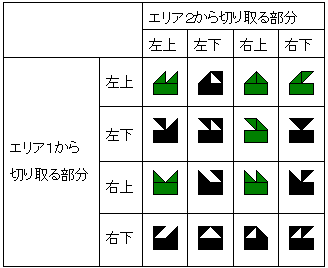
エリア 1 と エリア 2 から切り取る場合を考えると、次の表の 16 通りのうち、緑色に塗られた 6 通りが条件に合う。
エリアの組合せは 4 通りあるので、計 6×4=24 通り。
A-3) 対角の 2 つのエリアから 1 個ずつ切り取る場合:
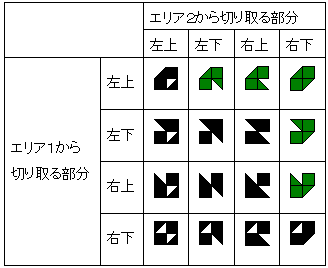
エリア 1 と エリア 3 から切り取る場合を考えると、次の表の 16 通りのうち、緑色に塗られた 5 通りが条件に合う。
エリアの組合せは 2 通りあるので、計 5×2=10 通り。
以上を合わせて、A) の場合は 4+24+10=38 通り。
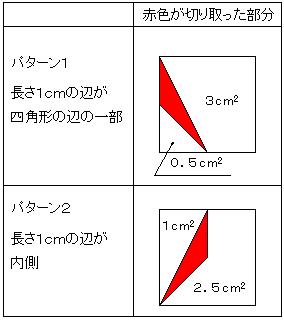
B) 三角形 1 と 三角形 2 を 1 個ずつ切り取る場合:
さきに 三角形 2 を切り取るとすると、その切り取り方は次の 2 パターンある。
- 長さ 1 cm の辺が四角形の辺の一部
- 長さ 1 cm の辺が四角形の内側
B-1) 長さ 1 cm の辺が四角形の辺の一部になっている場合:
残った部分は 3 cm² の四角形と 0.5 cm² の三角形に分割されているが、3 cm² の四角形を紙片とすればよい。三角形 2 の切り取り方は 8 通りあるので、面積が 3 cm² の紙片の切り取り方も 8 通り。
B-2) 長さ 1 cm の辺が四角形の内側にある場合:
残った部分は 1 cm² と 2.5 cm² の四角形に分割されている。このとき、3 cm² の四角形を切り取ることはできない。
C) 三角形 2 を 2 個切り取ることはできない。
A)~C) の場合を合わせて、38+8=46 (通り)
23. 流水算(ヒデー王子 さん)
ある川の川下の P 地点と川上の Q 地点の間を、静水時の速さの異なる船 A、B が進む。
ある日、両船が P 地点を Q 地点に向かって同時に出発し、途中船 A だけが 1 時間こぐのをやめて流されていたので、予定より 1 時間 15 分遅れて船 B と同時に Q 地点に到着した。またある日、両船が Q 地点を P 地点に向かって同時に出発し、途中船 A だけが 36 分間こぐのをやめて流されていたので、船 B と同時に P 地点に到着した。両船の静水時の速さは一定であるとし、流速も一定であるとする。
このとき次の問いに答えよ。
(1) 船 A の静水時の速さと流速の比を最も簡単な整数比で求めよ。
(2) P 地点から船 A が、Q 地点から船 B が同時に向かい合って出発するとすると、両船は何分後に出会うか。
〔解答・解説〕
(1) 等しい距離を、船 A が上る時間と川が流れる時間の比は (75-60):60=1:4 であるから、船 A の上りの速さと流速の比は 4:1
よって、船 A の静水時の速さと流速の比は (4+1):1=5:1
(2) 等しい距離を、船 B が上る時間と下る時間の比は 60:36=5:3 であるから、船 B の上りと下りの速さの比は 3:5
よって、船 B の静水時の速さと流速の比は {(5+3)÷2}:{(5-3)÷2}=4:1
(1) の結果と合わせて、
(船 A の静水時の速さ):(船 B の静水時の速さ):(流速)=5:4:1
したがって、両船が出会うのは
(4-1)×{60×5/(5-4)}÷(5+4)=100 (分後)
24. シェイクシェイク ?!(圭太 さん)
濃度の異なる砂糖水 A および B を 4:3 の比で混ぜて、濃度 15 % の砂糖水を作りたい。
A および B の濃度の組合せは何通りあるか。但し、どちらの砂糖水の濃度も、その百分比の値が整数値になるものに限る。また、濃度 0 % の場合は除く。
〔解答・解説〕砂糖水 A、B の濃度をそれぞれ a %、b % とする。
A を 4 kg、B を 3 kg 混ぜたとすると、砂糖水の量は 3+4=7 kg、その中に含まれる砂糖の量は 4×a/100+3×b/100=(4×a+3×b)/100、濃度は (4×a+3×b)/100÷7=(4×a+3×b)/700 である。
この値が 15 % に等しいから、(4×a+3×b)/700=15/100
すなわち、b=35-4/3×a
a、b は整数であるから、a は 3 の倍数である。…①
また、b>0 より、4/3×a<35
すなわち、a<105/4=26.25…②
①、②より、a のとりうる値は 1≦a≦26 を満たす 3 の倍数である。
したがって、(a,b) の組合せは (3,31)、(6,27)、(9,23)、(12,19)、(15,15)、(18,11)、(21,7)、(24,3) のうち、(15,15) を除く 7 通り。
25. 気付けば「秒殺」の平面図形(トトロ@N さん)
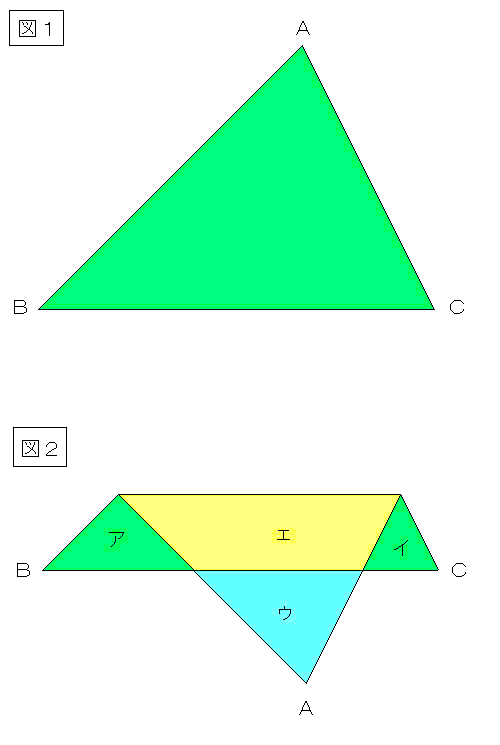
図 1 の三角形 ABC を、辺 BC に平行な直線で折り曲げると、図 2 のようになり、図 2 で、(三角形アの面積+三角形イの面積):(三角形ウの面積)=8:9 となりました。
このとき、(図 1 の三角形 ABC の面積):(図 2 の台形エの面積) を最も簡単な整数比で求めなさい。ただし、台形エは、三角形 ABC を折り曲げたときに重なった部分です。
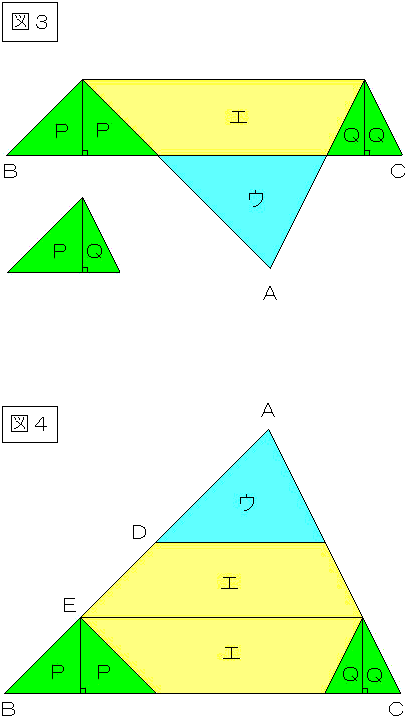
〔解答・解説〕図 3 のように、2 つの三角形 ア、イ の頂点から底辺に垂線を下ろすと、それぞれ合同な三角形に 2 等分される。2 等分された三角形をそれぞれ P、Q とすると、図 3 のようにそれらを合わせた三角形と三角形 ウ の面積比は (8÷2):9=4:9 である。相似比は 2:3 であるから、図 4 において、AD:DE:EB=3:2:2
したがって、(三角形 ABC の面積):(台形 エ の面積)=(7×7):(5×5-3×3)=49:16
26. 数字遊びはお好き?(僕は好き)(AЯOT さん)
0~9 の 10 個の数字を 1 回ずつ使って次のような 10 桁の整数を作ります。
- 整数の上から 2 桁を取り出した数は 2 で割り切れる。
- 整数の上から 3 桁を取り出した数は 3 で割り切れる。
- 整数の上から 4 桁を取り出した数は 4 で割り切れる。
- 整数の上から 5 桁を取り出した数は 5 で割り切れる。
- 整数の上から 6 桁を取り出した数は 6 で割り切れる。
- 整数の上から 7 桁を取り出した数は 7 で割り切れる。
- 整数の上から 8 桁を取り出した数は 8 で割り切れる。
- 整数の上から 9 桁を取り出した数は 9 で割り切れる。
- 整数全体は 10 で割り切れる。
この整数は何ですか?
〔解答・解説〕10 けたの整数を "ABCDEFGHIJ" とする。
10 けたの整数は 10 の倍数であるから、一の位 J は 0 である。
また、上から 5 けたが 5 の倍数であるから、E は 5 である。
さらに、上から 2、4、6、8 けた目 の B、D、F、H には偶数 2、4、6、8 のいずれかが割り当てられ、残りの A、C、G、I には奇数 1、3、7、9 のいずれかが割り当てられる。
このことを次のような表にまとめる。
| A | B | C | D | E | F | G | H | I | J |
| 1 | 1 | 1 | 1 | ||||||
| 2 | 2 | 2 | 2 | ||||||
| 3 | 3 | 3 | 3 | ||||||
| 4 | 4 | 4 | 4 | ||||||
| 5 | |||||||||
| 6 | 6 | 6 | 6 | ||||||
| 7 | 7 | 7 | 7 | ||||||
| 8 | 8 | 8 | 8 | ||||||
| 9 | 9 | 9 | 9 | ||||||
| 0 |
上から 4 けたが 4 の倍数であるから、"CD" は 4 の倍数である。
ところが、D が 4 または 8 のときは適当な C が存在しないので、D は 4 または 8 ではない。
"GH" も 4 の倍数であるが、同様の理由で H は 4 または 8 ではない。
| A | B | C | D | E | F | G | H | I | J |
| 1 | 1 | 1 | 1 | ||||||
| 2 | 2 | 2 | 2 | ||||||
| 3 | 3 | 3 | 3 | ||||||
| 4 | 4 | ||||||||
| 5 | |||||||||
| 6 | 6 | 6 | 6 | ||||||
| 7 | 7 | 7 | 7 | ||||||
| 8 | 8 | ||||||||
| 9 | 9 | 9 | 9 | ||||||
| 0 |
上から 3 けた目までの和 A+B+C、および上から 6 けた目までの和 A+B+C+D+E+F はともに 3 の倍数であるから、D+E+F は 3 の倍数である。
よって、"DEF" は 258 または 654 である。
1) "DEF" が 258 の場合:
| A | B | C | D | E | F | G | H | I | J |
| 1 | 1 | 1 | 1 | ||||||
| 2 | |||||||||
| 3 | 3 | 3 | 3 | ||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 | 7 | 7 | 7 | ||||||
| 8 | |||||||||
| 9 | 9 | 9 | 9 | ||||||
| 0 |
"ABC" は 3 の倍数であるから、147 または 741
また、上から 8 けたが 8 の倍数であるから、"FGH" は 8 の倍数、すなわち 816 または 896
よって、G は 9 となる。このとき、上から 7 けたは 1472589 または 7412589 となるが、いずれも 7 の倍数ではない。
2) "DEF" が 654 の場合:
| A | B | C | D | E | F | G | H | I | J |
| 1 | 1 | 1 | 1 | ||||||
| 2 | |||||||||
| 3 | 3 | 3 | 3 | ||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 | 7 | 7 | 7 | ||||||
| 8 | |||||||||
| 9 | 9 | 9 | 9 | ||||||
| 0 |
上から 8 けたが 8 の倍数であるから、"FGH" は 8 の倍数、すなわち 432 または 472
2-a) "FGH" が 432 の場合:
| A | B | C | D | E | F | G | H | I | J |
| 1 | 1 | 1 | |||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 | 7 | 7 | |||||||
| 8 | |||||||||
| 9 | 9 | 9 | |||||||
| 0 |
"ABC" は 3 の倍数であるから、189、981、789、987 のいずれか。
よって、上から 7 けたは 1896543、9816543、7896543、9876543 のいずれかとなるが、いずれも 7 の倍数ではない。
2-b) "FGH" が 472 の場合:
| A | B | C | D | E | F | G | H | I | J |
| 1 | 1 | 1 | |||||||
| 2 | |||||||||
| 3 | 3 | 3 | |||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 | |||||||||
| 8 | |||||||||
| 9 | 9 | 9 | |||||||
| 0 |
"ABC" は 3 の倍数であるから、183、381、189、981 のいずれか。
よって、上から 7 けたは 1836547、3816547、1896547、9816547 のいずれかとなるが、このうち 3816547 が 7 の倍数である。
以上より、すべての条件を満たす整数は 3816547290 である。
27. 2002 FIFA World Cup Korea/Japan 記念問題(ミミズクはくず耳 さん)

サッカーワールドカップの日韓共同開催にあたって、日韓のユニホームカラーの青と赤に塗った記念ボールを作ることにしました。図の様に、サッカーボールは正六角形 20 個と正五角形 12 個を組み合わせた形をしていて、クラシックなものは正五角形を黒、正六角形を白に塗ってあります。
記念ボールでは、両国を平等に、正五角形 12 個の内 6 個を日本の青に、残り 6 個を韓国の赤に塗り分けることにします。正六角形は全部白に塗ります。
さて、全部で何種類の記念ボールができるでしょうか。
補足:回転して同じになるものは、1 種類とします。右手と左手の様に、左右対称でも回転して同じにならないものは別に数えます。サッカーボールの 展開図 を添付しますので、お時間のある方は模型を組み立ててお考え下さい。
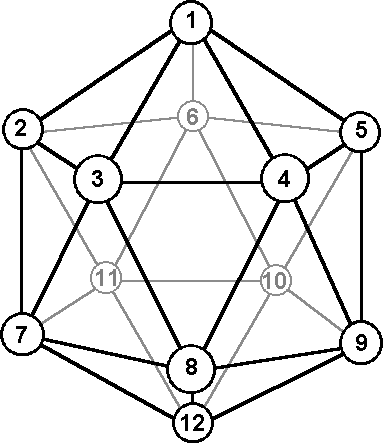
〔解答・解説〕サッカーボールは正二十面体の各頂点を切り落とした立体である。この問題では、サッカーボールの形で考えるより、「正二十面体の 12 個の頂点から 6 個を選ぶ」と考えたほうが分かりやすい。(展開図の組み立ても簡単です)
下図のように、正二十面体の 12 個の頂点に番号をつける。これらの頂点から 6 個を選んだとき、同一面の 3 個の頂点すべてが選ばれた面(三角形)の数で分類する。
- 三角形が 5 面の場合:
(1,2,3,4,5,6) の 1 種類 - 三角形が 4 面の場合:
(1,2,3,4,5,7)、(1,2,3,4,5,8)、(1,2,3,4,5,9) の 3 種類 - 三角形が 3 面の場合:
(1,2,3,4,5,10)、(1,2,3,4,5,11)、(1,2,3,4,5,12) の 3 種類 - 三角形は 2 面で,それらの面が隣り合っている場合:
(1,2,3,4,9,10)、(1,2,3,4,9,12)、(1,2,3,4,9,11)、(1,2,3,4,10,12) の 4 種類 - 三角形は 2 面で,それらの面が離れている場合:
(1,2,3,9,10,12)、(1,2,3,5,9,10) の 2 種類 - 三角形が 1 面の場合:
(1,2,3,5,8,11)、(1,2,3,8,9,10)、(1,2,3,9,10,11)、(1,2,3,5,8,9)、(1,2,3,5,8,10)、(1,2,3,5,8,12) の 6 種類 - 三角形は 0 面で,頂点を辺にそって結ぶと大きな閉じたループができる場合:
(1,3,8,12,10,6)、(1,3,8,9,10,6) の 2 種類 - 三角形は 0 面で,頂点を辺にそって結んでも閉じたループができない場合:
(1,3,8,9,10,11)、(1,4,8,7,11,10) の 2 種類 - 三角形は 0 面で,頂点を辺にそって結ぶと小さな閉じたループができる場合:
(2,3,4,5,6,12) の 1 種類
以上を合わせて、1+3+3+4+2+6+2+2+1=24 (種類)
でも、これで本当に数え落としがないのか不安ですね。
そこで、次のように考えます。
上図のように、正二十面体の各頂点に番号をつけて、それぞれを区別する場合を考えます。このとき、回転は考えません。12 個の頂点から 6 個を選ぶので、組合せの数は 12C6=12!/(6!×6!)=924 通りです。よって、上記 24 種類のパターン(順に、パターン 1、パターン 2、… ということにします)それぞれに対し、各頂点を区別して、同じ形の個数を数え上げて合計すれば 924 通りになるはずです。
まず、正二十面体を回転して自分自身と重なる場合は何通りあるか考えてみましょう。
上図を見てください。各頂点を区別するのですから、一番上にどの頂点がくるかで 12 通りあります。また、一番上の頂点が決まっても、上下を貫く軸で回転することができ、回転しない場合を含めて 5 通りあります(上図において、1 と 12 を通る直線を軸に回転すると、頂点②を②~⑥の各頂点に重ねることが可能です)。よって、正二十面体は 12×5=60 (通り) の回転による重ね合わせが可能です。
では、24 種類のパターンをそれぞれ見ていきましょう(解説図 を参照してください)。
パターン 1:
上下に対称軸があり、回転して自分と重なる場合は(回転しない場合を含めて)5 通り(1' 参照)。よって、頂点を区別する場合、パターン 1 と同じ形になる頂点の選び方(同じ形の数)は 60÷5=12 (通り)。あるいは、青色の頂点を決めると、パターン 1 の 6 個の選び方は一意に決まるので、正二十面体の頂点の数と同じ 12 通り。
パターン 2:
2 つの辺の中点を通る赤色の対称軸で 180 度回転すると重なるから、同じ形の数は 60÷2=30 (通り)。あるいは、パターン 2 の選び方は青色の辺と対応するので、辺の数と同じ 30 通り。
パターン 3:
2 つの面の重心を通る赤色の対称軸で ±120 度回転すると重なるから、同じ形の数は 60÷3=20 (通り)。あるいは、パターン 3 の選び方はパターンの中央の面と対応するので、面の数と同じ 20 通り。
パターン 4:
パターン 2 の鏡像で、2 と同じく 30 通り。
パターン 5:
回転して重ねることができるのは自分自身しかないので、頂点を区別する正二十面体の数と同じ 60 通り。
パターン 12 (20):
3 回対称の回転軸が 1 つと、2 回対称の回転軸が 3 つあるので、動かさない場合が 1、3 回対称で 2、2 回対称で 1×3 の計 6 通り重なる場合があるから、同じ形の数は 60÷6=10 (通り)。あるいは、向かい合っている 2 つの面を通る軸とパターン 12 が対応し、軸の数は面の数の半分であるから 20÷2=10 (通り)。
以下同様に、各パターンごとに表にまとめると、次のようになります。
24 種類のパターンの同じ形の数を合計すると 924 になり、最初に計算した 12C6 と同じになり、数え落としのないことが分かります。
ちなみに、黒白を入れ替えたときと、鏡像(右手 vs 左手)がどのパターンになるかも載せておきました。
| パターン番号 | 三角形の数 | 五角形の数 | 形 | 例 | 回転して自分と重なる数 | 同じ形の数 | 対応 | 黒 vs 白 | 右手 vs 左手 |
| 1 | 5 | 1 | (1,2,3,4,5,6) | 5 | 12 | 頂点 | 自分 | 自分 | |
| 2 | 4 | (1,2,3,4,5,7) | 2 | 30 | 辺 | 自分 | 4 | ||
| 3 | 4 | (1,2,3,4,5,8) | 3 | 20 | 面 | 自分 | 自分 | ||
| 4 | 4 | (1,2,3,4,5,9) | 2 | 30 | 辺 | 自分 | 2 | ||
| 5 | 3 | (1,2,3,4,5,10) | 1 | 60 | 自分 | 6 | |||
| 6 | 3 | (1,2,3,4,5,11) | 1 | 60 | 自分 | 5 | |||
| 7 | 3 | (1,2,3,4,5,12) | 1 | 60 | 17 | 自分 | |||
| 8 | 2 | 三角形 2 面が隣り合う | (1,2,3,4,9,10) | 1 | 60 | 自分 | 9 | ||
| 9 | 2 | (1,2,3,4,9,12) | 1 | 60 | 自分 | 8 | |||
| 10 | 2 | (1,2,3,4,9,11) | 2 | 30 | 辺 | 13 | 自分 | ||
| 11 | 2 | (1,2,3,4,10,12) | 2 | 30 | 辺 | 21 | 自分 | ||
| 12 | 2 | 三角形 2 面が分離 | (1,2,3,9,10,12) | 6 | 10 | 2 面 (軸) | 20 | 自分 | |
| 13 | 2 | (1,2,3,5,9,10) | 2 | 30 | 辺 | 10 | 自分 | ||
| 14 | 1 | (1,2,3,5,8,11) | 3 | 20 | 面 | 自分 | 自分 | ||
| 15 | 1 | (1,2,3,8,9,10) | 1 | 60 | 自分 | 16 | |||
| 16 | 1 | (1,2,3,9,10,11) | 1 | 60 | 自分 | 15 | |||
| 17 | 1 | 1 | (1,2,3,5,8,9) | 1 | 60 | 7 | 自分 | ||
| 18 | 1 | (1,2,3,5,8,10) | 1 | 60 | 自分 | 19 | |||
| 19 | 1 | (1,2,3,5,8,12) | 1 | 60 | 自分 | 18 | |||
| 20 | 0 | 閉じた大ループ | (1,3,8,12,10,6) | 6 | 10 | 2 面 (軸) | 12 | 自分 | |
| 21 | 0 | (1,3,8,9,10,6) | 2 | 30 | 辺 | 11 | 自分 | ||
| 22 | 0 | ループなし | (1,3,8,9,10,11) | 2 | 30 | 辺 | 自分 | 23 | |
| 23 | 0 | (1,4,8,7,11,10) | 2 | 30 | 辺 | 自分 | 22 | ||
| 24 | 0 | 1 | 閉じた小ループ | (2,3,4,5,6,12) | 5 | 12 | 頂点 | 自分 | 自分 |
| 合計 | 924 |
最後におまけです。
この問題とは逆に、正五角形 12 面を白く塗り、正六角形 20 面を青 10 面、赤 10 面に塗り分けると、なんと 3158 種類の記念ボールができます。
実は、「正五角形 12 面を濃い青 6 面、濃い赤 6 面に、正六角形 20 面を淡いブルー 10 面、淡いピンク 10 面に塗り分ける」という問題を最初に考えたのですが、とても解けなかったので、この問題になりました。
どなたか解けたら教えてください。<m(__)m>
28. 某中学校入試問題対策……ではないです。(地蔵 さん)
三角形 ABC において、∠A の二等分線と辺 BC の交点を D とすると、AB+AD=CD、AC+AD=BC となりました。このとき、∠ADB は何度ですか。
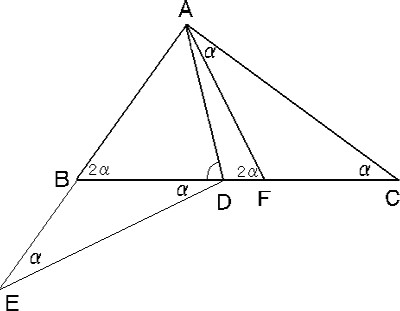
〔解答・解説〕∠CAB=∠A、∠ABC=∠B、∠ACB=∠C とかく。
AB+AD=CD…①、AC+AD=BC…②
②-① より、AC-AB=BC-CD=BD
辺 AB の延長線上に点 E を AE=AC となるようにとると、BE=AE-AB=AC-AB=BD となるので、三角形 BED は二等辺三角形となり、∠B=∠BED+∠BDE=∠AED×2
また、AE=AC、AD は共通、∠EAD=∠CAD より、三角形 AED と 三角形 ACD は合同。
よって、∠B=∠AED×2=∠C×2
∠C=α とする。
辺 BC 上に点 F を ∠FAC=α となるようにとると、∠FAC=∠ACF より 三角形 AFC は二等辺三角形となり、AF=CF
また、∠AFB=α×2=∠B であるから、AB=AF=CF
これと①より、DF=CD-CF=CD-AB=AD
よって、∠DAF=∠DFA=α×2
したがって、∠BAD=∠DAC=α×2+α=α×3、∠A=∠BAD+∠DAC=(α×3)×2=α×6
三角形 ABC の内角の和は 180° であるから、
∠A+∠B+∠C=α×6+α×2+α=α×9=180°
よって、α=20°
したがって、∠A=120°、∠B=40° となるので、
∠ADB=180°-(120°÷2+40°)=80°
29. 旧・第二種情報処理技術者試験(わかさひ君 さん)
あるコンピュータでのお話です。
パック型
| 00 | 01 | 23 |
アンパック型
| ?1 | ?2 | ?3 |
という 2 種類の整数型があり、このコンピュータでは上の例だとどちらも 123 という数値です。特にアンパック型は "?" の部分にはどんな数字が入っていても同じように解釈されます。つまり、具体的には
| 10 | 34 | 95 |
| 00 | 04 | 05 |
のどちらでも 45 と解釈されます。
(以下、これらの表記を [10 34 95]、[00 04 05] などと表すことにします。)
さて、このコンピュータには、「入力装置」、「変換装置 1」、「変換装置 2」、「演算装置」、「出力装置」の 5 つの装置があります。それぞれの装置の役割は次の通りです。
- 「入力装置」
この装置は、キーボードで入力した数値をアンパック型で渡してくれます。キーボードでの入力は 3 けたまで可能です。入力した結果渡されるアンパック型の "?" の部分には 1 けたの整数が入りますが、どの数字が入るかは分かりません。
例:キーボードで 123 を入力 → 「入力装置」 → [91 82 73](アンパック型) - 「変換装置 1」
この装置にアンパック型の整数を渡すと同じ数値を表すパック型に変換して返してくれます。このとき、アンパック型の "?" の部分は何が入っていても無視されます。
例:[12 34 56](アンパック型) → 「変換装置 1」 → [00 02 46](パック型) - 「変換装置 2」
この装置にパック型の整数を渡すと同じ数値を表すアンパック型に変換して返してくれます。このとき、アンパック型の "?" の部分には 1 けたの整数が入りますが、どの数字が入るかは分かりません。
例:[00 01 23](パック型) → 「変換装置 2」 → [41 52 63](アンパック型) - 「演算装置」
この装置は与えられた数をパック型と解釈して計算を行い、計算結果をパック型の表記で返してくれます。
例:[00 02 19] ÷ [00 00 02] → 「演算装置」 → [00 01 09] あまり [00 00 01] - 「出力装置」
この装置は与えられた数をアンパック型とみなして画面に表示します。
例:[74 85 96] → 「出力装置」 → 画面に 456 と表示される
つまり、このコンピュータで計算をしたければ、
(例:12 を入力して 12×12+12 を計算する)
| 「入力装置」で入力された数値を取得 | [10 21 32] |
| ↓ | ↓ |
| 「変換装置 1」でパック型に変換 | [00 00 12] |
| ↓ | ↓ |
| 「演算装置」で必要な計算 | [00 00 12] × [00 00 12] = [00 01 44] [00 01 44] + [00 00 12] = [00 01 56] |
| ↓ | ↓ |
| 「変換装置 2」でアンパック型に変換 | [91 85 76] |
| ↓ | ↓ |
| 「出力装置」に渡して表示 | 答えは 156(画面表示) |
という手順を踏む必要があります。
また、その計算ができないとき(0 で割り算をしようとした、小さい数から大きい数を引こうとした)、あるいは、計算した結果、パック型で 100 万以上になるときには「計算不可能」という報告をします。
さて問題です。このことを知らなかった W 君が作ったプログラムでは、以下の計算を型の変換をせずに行ってしまい、
- 「入力装置」からキーボードで入力された 2 つの数値を取得
- 「演算装置」でいろいろな計算
- 「出力装置」に渡して表示
としてしまいました。入力した数字は 2 種類で、それらを A、B とすると、
| 行った計算 | → | 画面表示 |
| A+B | → | 25 |
| A-B | → | 999 |
| A+A | → | 24 |
| B+B | → | 26 |
| A÷B | → | 66 あまり 14 |
| B÷A | → | 0 あまり 13 |
| B×B | → | 119 |
| A+A+A+A+A | → | 計算不可能 (パック型で 100 万以上の数になってしまった) ※ A+A+A+A までは計算できました。 |
となってしまいました。入力した数はそれぞれいくつだったでしょうか。
注 1:キーボードで入力した数を答えてください。
(パック型あるいはアンパック型の表現で答えるのではないことに注意してください)
注 2:2 つの数字をキーボードで入力したのは 1 回のみで、一度「入力装置」から取得した結果をすべての計算の A、B として共通に使用しています。
〔解答・解説〕B×B が 100 万以上でなかったことから、B のアンパック型表現は [00 10 00] より小さい。すなわち、入力された数 B は 100 未満である。また、A を 5 倍すると 100 万以上になったことから、A のアンパック型表現の十万の位は 2 である。(20 万未満のときは、5 倍しても 100 万を超えないし、30 万以上のときは、4 倍すると 100 万を超えてしまう。)
よって、アンパック型表現でも入力された数でも、A>B である。
A と B が等しくなければ、A÷B と B÷A の少なくとも一方の商は 0 であるが、B÷A の 結果から、B のアンパック型表現が [?0 ?1 ?3] であることが分かる。よって、入力された数 B は 13 である。
はじめの考察と合わせると、B のアンパック型表現は [00 01 ?3] とまで確定する。
また、A+B → 25 であることから、A の一の位は 2、アンパック型表現の一万の位は 0 である。すなわち、A のアンパック型表現は [20 ?? ?2] である。さらに、A+A → 24 であることから、A のアンパック型表現の百の位は 1 または 6 であるが、A+B → 25 であることから、A のアンパック型表現の百の位は 1 に決まる。よって、入力された数 A は 12 である。
したがって、答えは A が 12、B が 13 となる。
〔出題者からのコメント〕
変則的な虫食い算です。元ネタはメインフレームの 10 進数表現からです。今のシスアド試験にも出題されてるんじゃないかしらん?
30. 今回はオアシスになれるかな?(KIN さん)
算トラ IV で KIN 君は「平面 KIN マーク」を作り大満足♪
今でもズボンのひざの破けたところにはしっかりとアップリケがついています。
さて、1 年間の修行の末、今回算トラ V では「立体 KIN マーク」作成に燃えている KIN 君でありました。
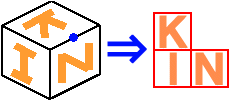
まずは、5 cm × 5 cm の方眼紙に "K"、"I"、"N" の文字を 1 枚ずつ、下図のようにデザインします。
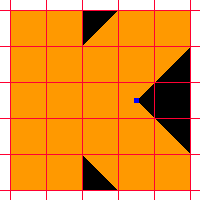
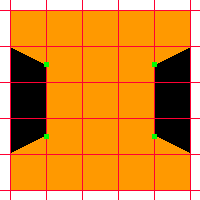
注意 1:図の黄緑色の点は 1 辺の中点、青色の点は 1 つのマスの中心です。
注意 2:図の 1 マスは 1 cm です。

次に、5 cm × 5 cm × 5 cm の立方体を用意し、"K"、"I"、"N" のデザインを描いた方眼紙を、6 面のうち 3 面にうら返しにしないように貼ります。ただし、立方体の向かい合った面に方眼紙を貼ってはいけません。
例えば、右図のような貼り方がありますね。
ここで、KIN 君はこの他にも文字を回転させたり、貼る面を変えたりすることにより、たくさんの貼り方があることに気がつきました。
方眼紙をはったら、それぞれのデザインの黒い部分を、その面と垂直に切り落とします。この作業を "K"、"I"、"N" の文字すべてについてやります。
この作業をすると、影絵として、「N」を貼った面から光を当てると「N」の文字が影として出てきますね。同様に、"K" の面から光を当てると "K" の文字、"I" の面からだと "I" という影絵ができます。
最後に、型紙にしていた方眼紙をはがしましょう。
これで、立体 KIN マークが完成しました。
わぁいヽ(∇⌒ヽ)(ノ⌒∇)ノわぁい♪
(1) 立体 KIN マークとして考えられる形は何通りありますか。ただし、回転して重なるものは 1 つと数えます。
(2) 右図のように方眼紙を貼った場合、切り落としの作業で完成した立体 KIN マークの体積は何 cm³ ですか。
〔解答・解説〕
(1) 図の左のように立方体を見て、青色の点がある辺で展開したときの位置関係を、図の右のように表すことにする。
文字を貼るときの向きや、貼る位置関係を変えると、次の 32 通りができる。







上図において、黒色の番号と青色の番号は同じ立体を表している。
2 段目の (5)~(8) はそれらを立体にして、左に 90 度回転させると、1 段目の (5)~(8) と一致する。
3 段目の (9)~(12) は それらを立体にして、左に 90 度回転させると、2 段目の (9)~(12) と一致する。
4 段目の (5)~(8) はそれらを立体にして、左に 90 度回転させると、3 段目の (5)~(8) と一致する。
4 段目の (1)~(4) はそれらを立体にして、右に 90 度回転させると、1 段目の (1)~(4) と一致する。
3 段目の (5)~(8) はそれらを立体にして、反対側から見ると、1 段目の (5)~(8) と一致する。
よって、12 通り。
(2) 上の段から立方体の状態を考えていくと、下図(左下のピンク色の点が正面)のようになる。①~③ はそれぞれ 1~3 段目の状態(単位は cm³)を表している。4、5 段目はそれぞれ 2、1 段目と同じ。
1 段目 は (21+1/2) cm³、2 段目は (14+1/2+7/12) cm³、3 段目は (10+3/4) cm³
よって、(1 段目)×2+(2 段目)×2+(3 段目)=1007/12 (cm³)


31. 四角形の面積は?(ジン ハジメ さん)
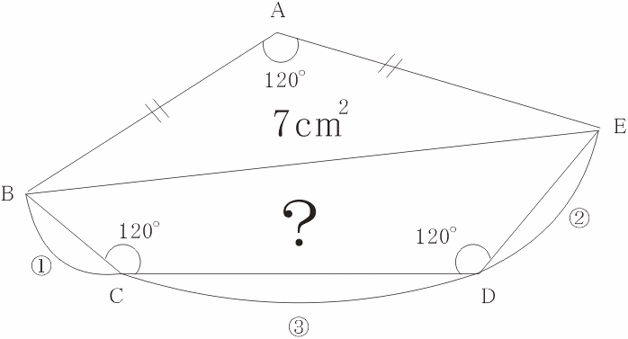
図のような五角形 ABCDE があります。AB と AE の長さが等しい二等辺三角形 ABE の面積が 7 cm²、∠BAE=∠BCD=∠CDE=120 度、BC:CD:DE=1:3:2 であるとき、四角形 BCDE の面積は何 cm² ですか。
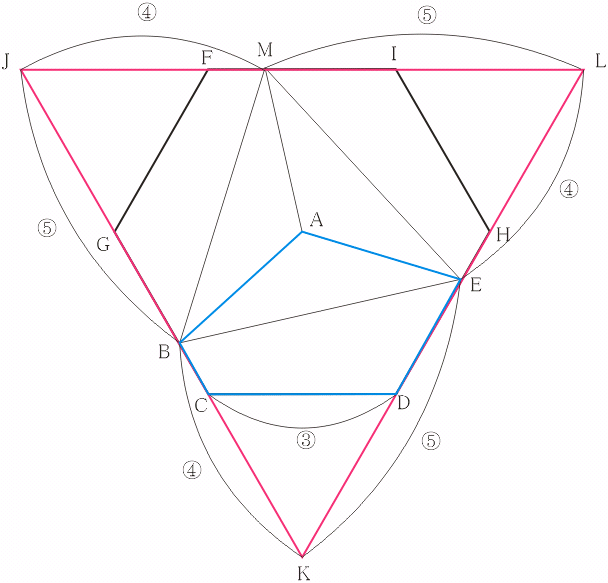
〔解答・解説〕五角形 ABCDE を 3 個くっつけて、正六角形 FGCDHI をつくる。
また、FI、GC、DH を延長して、正三角形 JKL をつくる。
三角形 KLJ の面積を 9×9=81 (cm²) とすると、三角形 KEB、JBM、LME は 4×5=20 (cm²)、三角形 KDC、JGF、LIH は 3×3=9 (cm²)、四角形 ABKE は 81÷3=27 (cm²) となる。
よって、(三角形 ABE)=(四角形 ABKE)-(三角形 KEB)=27-20=7 (cm²)、(四角形 BCDE)=(三角形 KEB)-(三角形 KDC)=20-9=11 (cm²)
したがって、(三角形 ABE):(四角形 BCDE)=7:11 であるから、四角形 BCDE の面積は 11 cm²
32. めちゃくちゃ大きいです(いやマジで)(HAL さん)
1~10 の整数のいずれかが書かれた 10 種類のカードを、次のように 1 列に並べました。
- まず、1 のカードを 10 枚 1 列に並べます。
- 次に、2 のカードをその間に 1 枚ずつ入れます。
- 次に、3 のカードを今まで並べたすべてのカードの間に 2 枚ずつ入れます。
- 次に、4 のカードを今まで並べたすべてのカードの間に 3 枚ずつ入れます。
- ……
このようにして、最後の 10 のカードをすべてのカードの間に 9 枚ずつ入れます。
このとき、カードは全部で何枚並べましたか。
〔解答・解説〕間の数は、2 のカードを入れると 2 倍、3 のカードを入れると 3 倍、… となっていく。よって、9×2×3×4×5×6×7×8×9×10+1=32659201 (枚)
33. 4 人組パーティ(杉本 未来 さん)
次の推理パズルを解いてください。
ある世界に、悪者をやっつけるために旅をしている 4 人組がいるそうです。
次の 9 つのヒントをもとにして、4 人の名前、年齢、職業、出身地、装備している武器の正しい組み合わせを推理してください。ただし、それらの内容は〈一覧〉にある通りで、別の人が同じ項目にあてはまることはないものとします。(つまり、バラバラです。)
注意:このような組み合わせはただ 1 通りのみ存在します。
〈一覧〉
- 名前(順不同):
オブセル コルプス サピエス フロール - 年齢(順不同):
17 歳 19 歳 21 歳 23 歳 - 職業(順不同):
ナイト シーフ 白魔道士 黒魔道士 - 出身地(順不同):
アリカル キローネ スラーク テーベ - 装備している武器(順不同):
オベリスク ルーンスタッフ ミスリルソード アサシンダガー
〈条件〉
- 白魔道士は 21 歳である。
- シーフの武器はアサシンダガーである。
- ナイトはテーベの出身だが、最年長ではない。
- ミスリルソードを装備している人の年齢は 19 歳である。
- ルーンスタッフを装備している人は最年少ではない。
- フロールはコルプスより 2 歳年上である。
- アリカル出身の人は、キローネ出身の人より年上である。
- スラーク出身の人は、オブセルより 2 歳年上である。
- オベリスクを装備している人は、サピエスより 4 歳年上である。
(1) 次のうち、10 代である 2 人の組み合わせを 1 つ選んでください。
- オブセル、コルプス
- オブセル、サピエス
- オブセル、フロール
- コルプス、サピエス
- コルプス、フロール
- サピエス、フロール
(2) 次のうち、魔道士である 2 人の組み合わせを 1 つ選んでください。
- オブセル、コルプス
- オブセル、サピエス
- オブセル、フロール
- コルプス、サピエス
- コルプス、フロール
- サピエス、フロール
※ 必要ならば下表をお使いください。
| 年齢 | 職業 | 出身地 | 武器 | ||||||||||||||
| 17 歳 |
19 歳 |
21 歳 |
23 歳 |
ナ イ ト |
シ | フ |
白 魔 道 士 |
黒 魔 道 士 |
ア リ カ ル |
キ ロ | ネ |
ス ラ | ク |
テ | ベ |
オ ベ リ ス ク |
ル | ン ス タ ッ フ |
ミ ス リ ル ソ | ド |
ア サ シ ン ダ ガ | | ||
| 名 前 |
オブセル | ||||||||||||||||
| コルプス | |||||||||||||||||
| サピエス | |||||||||||||||||
| フロール | |||||||||||||||||
| 武 器 |
オベリスク | ||||||||||||||||
| ルーンスタッフ | |||||||||||||||||
| ミスリルソード | |||||||||||||||||
| アサシンダガー | |||||||||||||||||
| 出 身 地 |
アリカル | ||||||||||||||||
| キローネ | |||||||||||||||||
| スラーク | |||||||||||||||||
| テーベ | |||||||||||||||||
| 職 業 |
ナイト | ||||||||||||||||
| シーフ | |||||||||||||||||
| 白魔道士 | |||||||||||||||||
| 黒魔道士 | |||||||||||||||||
〔解答・解説〕条件にしたがって、表に ○ と × を書き込んでいく。
条件 1 「白魔道士は 21 歳である。」より、
A に ○ が、a に × がつけられる。
条件 2 「シーフの武器はアサシンダガーである。」より、
B に ○ が、b に × がつけられる。
条件 3 「ナイトはテーベの出身だが、最年長ではない。」より、
C に ○ が、c に × がつけられる。
条件 4 「ミスリルソードを装備している人の年齢は 19 歳である。」より、
D に ○ が、d に × がつけられる。
条件 5 「ルーンスタッフを装備している人は最年少ではない。」より、
e に × がつけられる。
| 年齢 | 職業 | 出身地 | 武器 | ||||||||||||||
| 17 歳 |
19 歳 |
21 歳 |
23 歳 |
ナ イ ト |
シ | フ |
白 魔 道 士 |
黒 魔 道 士 |
ア リ カ ル |
キ ロ | ネ |
ス ラ | ク |
テ | ベ |
オ ベ リ ス ク |
ル | ン ス タ ッ フ |
ミ ス リ ル ソ | ド |
ア サ シ ン ダ ガ | | ||
| 名 前 |
オブセル | ||||||||||||||||
| コルプス | |||||||||||||||||
| サピエス | |||||||||||||||||
| フロール | |||||||||||||||||
| 武 器 |
オベリスク | d | b | ||||||||||||||
| ルーンスタッフ | e | d | b | ||||||||||||||
| ミスリルソード | d | D | d | d | b | ||||||||||||
| アサシンダガー | d | b | B | b | b | ||||||||||||
| 出 身 地 |
アリカル | c | |||||||||||||||
| キローネ | c | ||||||||||||||||
| スラーク | c | ||||||||||||||||
| テーベ | c | C | c | c | c | ||||||||||||
| 職 業 |
ナイト | a | c | ||||||||||||||
| シーフ | a | ||||||||||||||||
| 白魔道士 | a | a | A | a | |||||||||||||
| 黒魔道士 | a | ||||||||||||||||
条件 6 「フロールはコルプスより 2 歳年上である。」より、フロールは 17 歳でないことと、コルプスが 23 歳でないことがわかる。
よって、f に × がつけられる。
条件 7 「アリカル出身の人は、キローネ出身の人より年上である。」より、アリカル出身の人は 17 歳でないことと、キローネ出身の人が 23 歳でないことがわかる。
よって、g に × がつけられる。
条件 8 「スラーク出身の人は、オブセルより 2 歳年上である。」より、スラーク出身の人は 17 歳でないことと、オブセルが 23 歳でないことがわかる。
また、オブセルがスラーク出身でないこともわかる。
よって、h に × がつけられる。
条件 9 「オベリスクを装備している人は、サピエスより 4 歳年上である。」より、オベリスクを装備している人は 17 歳、19 歳でないことと、サピエスが 21 歳、23 歳でないことがわかる。
よって、i に × がつけられる。
ここで表を見ると、フロールが 23 歳であることがわかる。
したがって、J に ○ が、j に × がつけられる。
| 年齢 | 職業 | 出身地 | 武器 | ||||||||||||||
| 17 歳 |
19 歳 |
21 歳 |
23 歳 |
ナ イ ト |
シ | フ |
白 魔 道 士 |
黒 魔 道 士 |
ア リ カ ル |
キ ロ | ネ |
ス ラ | ク |
テ | ベ |
オ ベ リ ス ク |
ル | ン ス タ ッ フ |
ミ ス リ ル ソ | ド |
ア サ シ ン ダ ガ | | ||
| 名 前 |
オブセル | h | h | ||||||||||||||
| コルプス | f | ||||||||||||||||
| サピエス | i | i | |||||||||||||||
| フロール | f | j | j | J | |||||||||||||
| 武 器 |
オベリスク | i | × | × | |||||||||||||
| ルーンスタッフ | × | × | × | ||||||||||||||
| ミスリルソード | × | ○ | × | × | × | ||||||||||||
| アサシンダガー | × | × | ○ | × | × | ||||||||||||
| 出 身 地 |
アリカル | g | × | ||||||||||||||
| キローネ | g | × | |||||||||||||||
| スラーク | h | × | |||||||||||||||
| テーベ | × | ○ | × | × | × | ||||||||||||
| 職 業 |
ナイト | × | × | ||||||||||||||
| シーフ | × | ||||||||||||||||
| 白魔道士 | × | × | ○ | × | |||||||||||||
| 黒魔道士 | × | ||||||||||||||||
ここで表に目を移すと、次のように ○ と × がつけられる。
| 年齢 | 職業 | 出身地 | 武器 | ||||||||||||||
| 17 歳 |
19 歳 |
21 歳 |
23 歳 |
ナ イ ト |
シ | フ |
白 魔 道 士 |
黒 魔 道 士 |
ア リ カ ル |
キ ロ | ネ |
ス ラ | ク |
テ | ベ |
オ ベ リ ス ク |
ル | ン ス タ ッ フ |
ミ ス リ ル ソ | ド |
ア サ シ ン ダ ガ | | ||
| 名 前 |
オブセル | × | × | × | |||||||||||||
| コルプス | × | × | |||||||||||||||
| サピエス | × | × | × | ||||||||||||||
| フロール | × | × | × | ○ | × | × | × | ○ | × | × | × | × | |||||
| 武 器 |
オベリスク | × | × | × | × | × | × | ||||||||||
| ルーンスタッフ | × | × | × | × | × | × | |||||||||||
| ミスリルソード | × | ○ | × | × | ○ | × | × | × | × | × | × | ○ | |||||
| アサシンダガー | ○ | × | × | × | × | ○ | × | × | × | ○ | × | × | |||||
| 出 身 地 |
アリカル | × | × | × | × | ||||||||||||
| キローネ | ○ | × | × | × | × | ○ | × | × | |||||||||
| スラーク | × | × | × | × | |||||||||||||
| テーベ | × | ○ | × | × | ○ | × | × | × | |||||||||
| 職 業 |
ナイト | × | ○ | × | × | ||||||||||||
| シーフ | ○ | × | × | × | |||||||||||||
| 白魔道士 | × | × | ○ | × | |||||||||||||
| 黒魔道士 | × | × | × | ○ | |||||||||||||
ここで、フロールが 23 歳であることから、コルプスは 21 歳とわかる。
| 年齢 | 職業 | 出身地 | 武器 | ||||||||||||||
| 17 歳 |
19 歳 |
21 歳 |
23 歳 |
ナ イ ト |
シ | フ |
白 魔 道 士 |
黒 魔 道 士 |
ア リ カ ル |
キ ロ | ネ |
ス ラ | ク |
テ | ベ |
オ ベ リ ス ク |
ル | ン ス タ ッ フ |
ミ ス リ ル ソ | ド |
ア サ シ ン ダ ガ | |
||
| 名 前 |
オブセル | × | × | × | × | × | × | × | × | ||||||||
| コルプス | × | × | ○ | × | × | × | ○ | × | × | × | × | × | |||||
| サピエス | × | × | × | × | × | × | × | × | |||||||||
| フロール | × | × | × | ○ | × | × | × | ○ | × | × | × | × | |||||
| 武 器 |
オベリスク | × | × | × | × | × | × | ||||||||||
| ルーンスタッフ | × | × | × | × | × | × | |||||||||||
| ミスリルソード | × | ○ | × | × | ○ | × | × | × | × | × | × | ○ | |||||
| アサシンダガー | ○ | × | × | × | × | ○ | × | × | × | ○ | × | × | |||||
| 出 身 地 |
アリカル | × | × | × | × | ||||||||||||
| キローネ | ○ | × | × | × | × | ○ | × | × | |||||||||
| スラーク | × | × | × | × | |||||||||||||
| テーベ | × | ○ | × | × | ○ | × | × | × | |||||||||
| 職 業 |
ナイト | × | ○ | × | × | ||||||||||||
| シーフ | ○ | × | × | × | |||||||||||||
| 白魔道士 | × | × | ○ | × | |||||||||||||
| 黒魔道士 | × | × | × | ○ | |||||||||||||
ここまで出れば答えは出せますが、一応続けます。(^^ゞ
さらに、オブセルが 17 歳か 19 歳、スラーク出身の人が 21 歳か 23 歳であることから、オブセルは 19 歳、スラーク出身の人は 21 歳であることがわかる。
| 年齢 | 職業 | 出身地 | 武器 | ||||||||||||||
| 17 歳 |
19 歳 |
21 歳 |
23 歳 |
ナ イ ト |
シ | フ |
白 魔 道 士 |
黒 魔 道 士 |
ア リ カ ル |
キ ロ | ネ |
ス ラ | ク |
テ | ベ |
オ ベ リ ス ク |
ル | ン ス タ ッ フ |
ミ ス リ ル ソ | ド |
ア サ シ ン ダ ガ | | ||
| 名 前 |
オブセル | × | ○ | × | × | ○ | × | × | × | × | × | × | ○ | × | × | ○ | × |
| コルプス | × | × | ○ | × | × | × | ○ | × | × | × | ○ | × | ○ | × | × | × | |
| サピエス | ○ | × | × | × | × | ○ | × | × | × | ○ | × | × | × | × | × | ○ | |
| フロール | × | × | × | ○ | × | × | × | ○ | ○ | × | × | × | × | ○ | × | × | |
| 武 器 |
オベリスク | × | × | ○ | × | × | × | ○ | × | × | × | ○ | × | ||||
| ルーンスタッフ | × | × | × | ○ | × | × | × | ○ | ○ | × | × | × | |||||
| ミスリルソード | × | ○ | × | × | ○ | × | × | × | × | × | × | ○ | |||||
| アサシンダガー | ○ | × | × | × | × | ○ | × | × | × | ○ | × | × | |||||
| 出 身 地 |
アリカル | × | × | × | ○ | × | × | × | ○ | ||||||||
| キローネ | ○ | × | × | × | × | ○ | × | × | |||||||||
| スラーク | × | × | ○ | × | × | × | ○ | × | |||||||||
| テーベ | × | ○ | × | × | ○ | × | × | × | |||||||||
| 職 業 |
ナイト | × | ○ | × | × | ||||||||||||
| シーフ | ○ | × | × | × | |||||||||||||
| 白魔道士 | × | × | ○ | × | |||||||||||||
| 黒魔道士 | × | × | × | ○ | |||||||||||||
逆にこのとき、9 つの条件をすべて満たす。
したがって、答えは (1) b (2) e となる。
34. どっちも・たしま・SHOW!!(POI さん)
各位の数の和が 10 である 4 けたの整数 A と、各位の数の和が 7 である 4 けたの整数 B があります。A と B を加えると 3824 となり、A と B の差は偶数となりました。
このような (A,B) の組合せは何通りですか。
〔解答・解説〕A と B の差が偶数であることは自明。
A の各位の和が 10、B の各位の和が 7、そして合計の各位の和が 3+8+2+4=17 であることから、A と B を足すときに「くりあがりがない」ことが分かる。
B に着目する。
B は 1□0△、1□1△、1□2△、2□0△、2□1△、2□2△ の 6 パターンが考えられ(□ は 8 以下、△ は 4 以下)、(□,△) の組合せは
- 1□0△ → (2,4)、(3,3)、(4,2)、(5,1)、(6,0) の 5 通り
- 1□1△ → (1,4)、(2,3)、(3,2)、(4,1)、(5,0) の 5 通り
- 1□2△ → (0,4)、(1,3)、(2,2)、(3,1)、(4,0) の 5 通り
- 2□0△ → (1,4)、(2,3)、(3,2)、(4,1)、(5,0) の 5 通り
- 2□1△ → (0,4)、(1,3)、(2,2)、(3,1)、(4,0) の 5 通り
- 2□2△ → (0,3)、(1,2)、(2,1)、(3,0) の 4 通り
以上を合わせて、5+5+5+5+5+4=29 (通り)
35. ミレニアム記念大時計(中村 明海 さん)
ある公園に、2001 年内の完成をめざし、ミレニアムを記念した大時計を建設中です。分針が 20.01 m、時針が 14.2 m、そして秒針が 24.6 m という巨大なものです。まだ、それぞれの針が進む速さは正確ではありません。なお、これらの針の長さは時計の中心から先端までの距離とします。
さて、この時計の 3 本の針の先端を結ぶ三角形が正三角形になるとき、その正三角形の面積は、1 辺の長さが 1 m の正三角形の面積の何倍ですか。ただし、正三角形の大きさがいくつか考えられる場合は、それらすべての面積を合計してください。
〔解答・解説〕1) 正三角形ができるようす:
時計の中心を O、時針・分針・秒針の先端をそれぞれ A、B、C とし、三角形 ABC が正三角形であるとする。三角形 OCP が正三角形となるように点 P をとると、三角形 OCA と 三角形 PCB は合同(2 辺夾角相等)であるから、PB=OA(時針)。
よって、点 B は、点 O を中心とする分針の長さ OB を半径とする円と、点 P を中心とする時針の長さ OA を半径とする円の交点である。
2 つの円の交点は 2 個(図の B と B')であるから、条件を満たす正三角形の大きさもこれら大小 2 種類だけである。
2) 大きい正三角形の面積 S:
図のように、点 A、B、C を中心に、点 O を時計回りに 60 度回転した点を、それぞれ Q、R、P とする。また、OA、OB、OC を 1 辺とする正三角形の面積を、それぞれ "あ"、"い"、"う"、三角形 OBC、三角形 OCA、三角形 OAB の面積を、それぞれ "ア"、"イ"、"ウ" とし、3 本の針を 3 辺とする三角形の面積を "え" とする。このとき、
- 四角形 OAQC に注目して、あ(AOQ)+え(COQ)=イ(OAC)+ウ(QAC)
- 四角形 OBRA に注目して、い(BOR)+え(AOR)=ウ(OBA)+ア(RBA)
- 四角形 OCPB に注目して、う(COP)+え(BOP)=ア(OCB)+イ(PCB)
これら 3 つの式を足すと、あ+い+う+え×3=(ア+イ+ウ)×2…①
ここで、S(ABC)=ア(OBC)+イ(OCA)+ウ(OAB) であるから、
①より、S=(あ+い+う+え×3)÷2…②
ここまでは、類題(別解)が 算チャレ 第 15 回 にありますのでご参考に。
3) 小さい正三角形の面積 T:
記号を 2) と同様に定義する。ただし、点 R は、点 B を中心に、点 O を反時計回りに 60 度回転した点とする。
- 四角形 OACQ に注目して、あ(OAQ)+ウ(CAQ)=え(QOC)+イ(AOC)
- 四角形 OBCR に注目して、い(OBR)+ウ(CBR)=え(ROC)+ア(BOC)
- 四角形 OCBP に注目して、う(OCP)-イ(BCP)=え(POB)+ア(COB)
これら 3 つの式を足すと、あ+い+う=え×3+(ア+イ-ウ)×2…③
ここで、T(ABC)=ア(OBC)+イ(OCA)-ウ(OAB) であるから、
③より、T=(あ+い+う-え×3)÷2…④
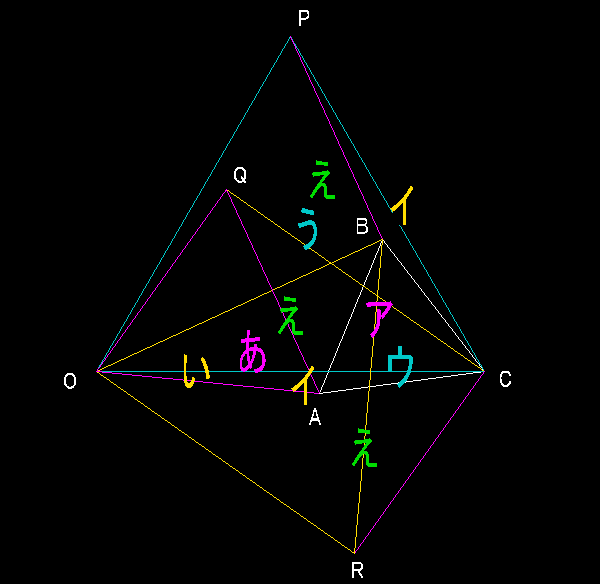
4) 正三角形の面積の合計:
大小の正三角形の面積の合計は、②+④より、S+T=あ+い+う
すなわち、それぞれの針の長さを 1 辺とする 3 個の正三角形の面積の和にほかならない。これらは、1 辺の長さが 1 m の正三角形の面積の、"あ" は 14.2×14.2=201.64 (倍)、"い" は 20.01×20.01=400.4001 (倍)、"う" は 24.6×24.6=605.16 (倍) である。
したがって、答えは 201.64+400.4001+605.16=1207.2001 (倍)
