A-01. 角の 3 等分(だいすけ さん)
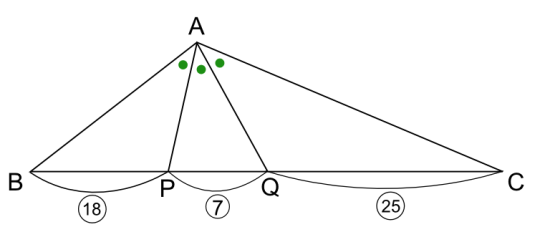
図のような三角形 ABC があります。
AP、AQ で角 A が 3 等分されるように、辺 BC 上に 2 点 P、Q をとると、BP:PQ:QC=18:7:25 となりました。
このとき、AP:AQ を最も簡単な整数比で答えてください。
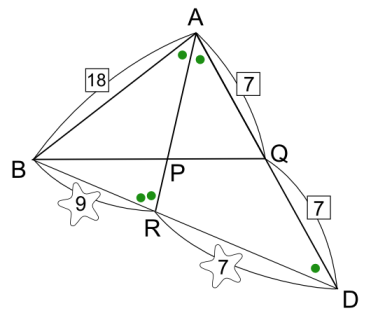
〔解答・解説〕まず、AB:AQ を求める。BP:PQ=18:7 であるから (三角形 ABP):(三角形 APQ)=18:7。ここで、点 P から AB、AQ にそれぞれ垂線 PH、PI を下ろすと、三角形 APH と三角形 API は合同であるから PH=PI。よって、AB:AQ=(三角形 ABP):(三角形 APQ)=18:7…(*)
同様にして、AP:AC=7:25…(**)
BQ=QC であるから、三角形 AQC を 180 度回転させると図のようになる。AP を延長して BD との交点を R とすると、(*) より AB:AQ=18:7 であるから AB:AD=9:7。よって、(*) と同様にして BR:RD=9:7。
三角形 BRA と三角形 BAD は相似であるから、BR/BA=BA/BD (=a とおく)。このとき、BR=BA×a=(BD×a)×a となり、BR:BD=9:16 であるから a=3/4。したがって、BA:BD=3:4。ゆえに、AB:AC=BA:BD=3:4…(***)
(*)、(**)、(***) より AQ:AB:AC:AP=175:450:600:168。ゆえに、AP:AQ=24:25
〔出題者からのコメント〕角の 2 等分線の定理を使わないと解けないかと思います。(*) 程度の内容なら、なんとか小学生でも考えられるかなぁと思い、出題しました。
考える糸口は、18+7=25 です。角の比 1:2 の使い方がポイントとなりますね。
〔寸評〕(難易度:★★★☆☆)
この問題の妙味は三角形を切り離して回転するところでしょう。角の 2 等分線の定理は中学の内容ですが、うまく解説されています。問題図が美しく描かれており、難易度も手ごろと思われましたので、栄えある第 1 問に選ばせていただきました。
A-02. 線分の長さの比は?(ごんごんま さん)
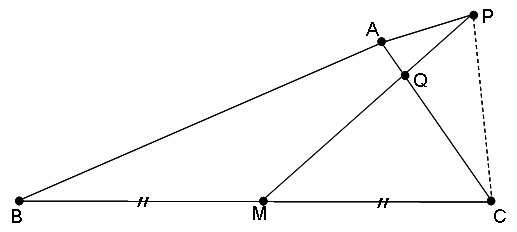
図のような三角形 ABC があります。
三角形 ABC の外部の点 P と頂点 A、また P と辺 BC のまん中の点 M を直線で結んだところ、PM は辺 AC と点 Q で交わり、AB:AQ:QC=21:1:8、PA:PQ:QM=2:2:7 となりました。
このとき、PC:AB を最も簡単な整数比で答えてください。
〔解答・解説〕PM を M の方に延長して PM=MR となる点 R をとると、三角形 BMP と三角形 CMR は合同であるから、BP と CR は平行である。また、三角形 AQP と三角形 CQR は相似(相似比は 1:8)であるから、AP と CR は平行である。よって、AP と BP は平行となり、3 点 P、A、B は同一直線上にあることがわかる。
三角形 AQP と三角形 CQR の相似比は 1:8 であるから AP:CR=1:8。これと BP=CR より、AP:AB=AP:(BP-AP)=AP:(CR-AP)=1:7…(*)。さらに、AB:AQ=21:1 であるから AP:AQ=3:1…(**)
三角形 ACP と三角形 APQ において、AC:AP=(AQ×9):(AQ×3)=3:1 であることと (**) により、三角形 ACP と三角形 APQ は相似で、相似比は 3:1 である。よって、CP:PQ=3:1。これと AP=PQ より、CP:AP=3:1…(***)
(*) と (***) より、PC:AB=(AP×3):(AP×7)=3:7
〔寸評〕(難易度:★★★★☆)
この問題は 3 点 P、A、B が同一直線上にあることを見出すことがポイントになりますので、問題図はあえて微妙に不正確なものになっています。辺の比を問う問題を 2 題並べてみましたが、こちらは相当の難問と思われます。
A-03. いつになったら着くのやら(ほげ さん)
T 君が限りなく広い平らな原っぱのまん中で次のように動きます。
- まっすぐ 2 m 進んで止まります。
- 止まった地点で、その場で時計回りに 167.7 度まわります。
- 1.、2. の動きをくり返します。
このとき、T 君が最初にいた地点にはじめてもどるまでに進む距離は何 m ですか。ただし、最初にいた地点にもどることがないときは 0 と答えてください。
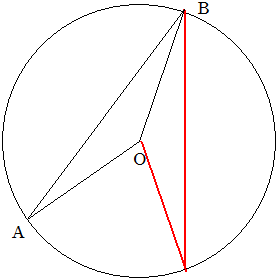
〔解答・解説〕T 君が止まるのは、ある円の円周上である。底辺 AB が 2 m、等しい角を (180°-167.7°)÷2=6.15° とする二等辺三角形 OAB と、その頂点 O を中心とし辺 OA を半径とする円を考える。このとき、三角形 OAB を点 O を中心として時計回りに(以下同様)167.7° 回転させると、点 A は点 B に重なり、点 B は点 C に移るとする。
T 君が点 A を出発して点 B で止まるとすると、次に止まるのは点 C である。さらに次に止まるのは、三角形 OBC を点 O を中心として 167.7° 回転させたときの点 C の移る点である。このようにして止まる点に着目すると、1 回の移動で点 O を中心として 167.7° 回転させた点へ移ることになる。よって、T 君が最初にいた地点にもどるためには、167.7=(3×13×43)/10 にある自然数をかけたとき 360 の整数倍になればよい。n×(3×13×43)/(10×360) が整数になるような最小の自然数 n は 1200 であるから、T 君が最初にいた地点にはじめてもどるまでに進む距離は 2×1200=2400 (m)。
〔寸評〕(難易度:★★★☆☆)
T 君はジグザグに進むのですが、止まる地点がある円の円周上であるのは面白いですね。後半は整数の問題となりますが、この問題の本質は前半部にあると判断し、平面図形の領域に分類しました。
A-04. クッキーの大きさ(なか さん)
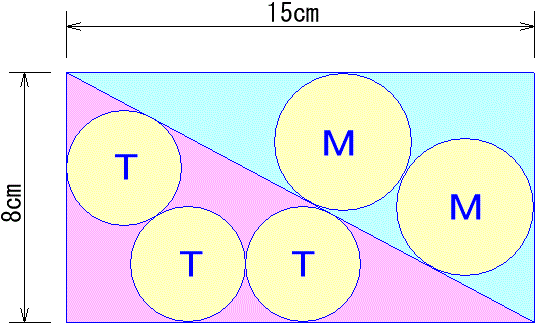
マサルさんとトモエさんがクッキー作りに挑戦しています。
まず、たて 8 cm、横 15 cm の長方形の生地を作り、うらみっこなしに対角線で切って半分こしました。対角線の長さは 17 cm だったそうです。
次に、直角三角形の生地から円形を切りぬきます。マサルさんは 2 つの円 M を、トモエさんは 3 つの円 T を、それぞれ図のように切りぬきました。ふたりとも目いっぱいの大きさに切りぬき、ひとりが切った円の大きさはそろっています。
お互いに「こっちの方が大きいぞ」と言い張っています。どちらが大きいか正確に判定したいと思います。
トモエさんの円 3 個分は、マサルさんの円 2 個分の何倍ですか。
〔解答・解説〕
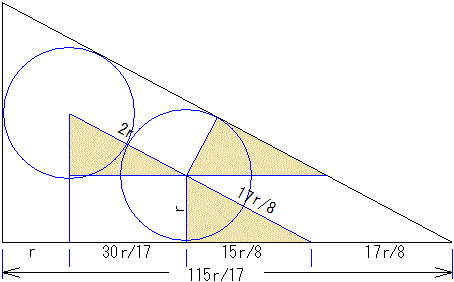
1) マサルさんのクッキー
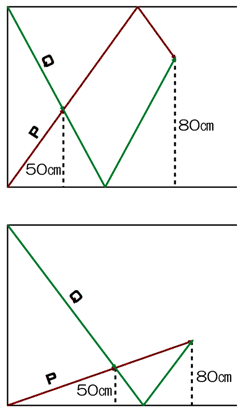
2 つの円の中心からもとの直角三角形の 3 辺に平行または垂直な直線を図のようにひくと、もとの直角三角形と相似な三角形があちこちにできる。円の半径を r cm とすると、上図の底辺は r×(115/17) cm である。r×(115/17)=15 より r=51/23 である。
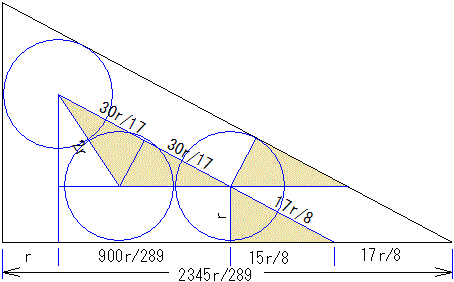
2) トモエさんのクッキー
3 つの円の中心からもとの直角三角形の 3 辺に平行または垂直な直線を図のようにひくと、もとの直角三角形と相似な三角形があちこちにできる。円の半径を r cm とすると、上図の底辺は r×(2345/289) cm である。r×(2345/289)=15 より r=867/469 である。
3) 大きさの比較
867=51×17 に注意すると、2 つの円の半径の比は (867/469):(51/23)=(17/469):(1/23)=391:469。よって、面積の比は (391×391×3):(469×469×2)=458643:439922 である。ゆえに、トモエさんの円 3 個分はマサルさんの円 2 個分の 458643/439922 倍であり、トモエさんの勝ちである。
〔寸評〕(難易度:★★☆☆☆)
直角三角形の内部に各辺と平行な補助線を引き、相似な三角形を考えるのは比較的容易ですが、分数計算はていねいに行う必要があります。今回の大会では答えの数値が最も複雑な問題です。
A-05. 角度の問題です(Zambara さん)
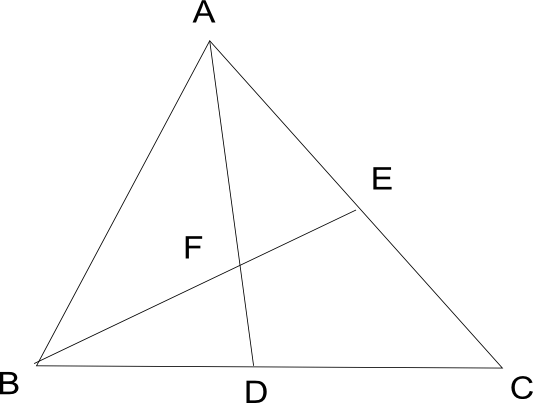
図のような、角 A の大きさが 64 度 である三角形 ABC があります。
角 A を 2 等分する直線と辺 BC の交点を D、角 B を 2 等分する直線と辺 AC の交点を E とすると、AB+BD=AE+EB となりました。
AD と BE の交点を F とすると、角 DFE は何度ですか。ただし、図は正確とは限りません。
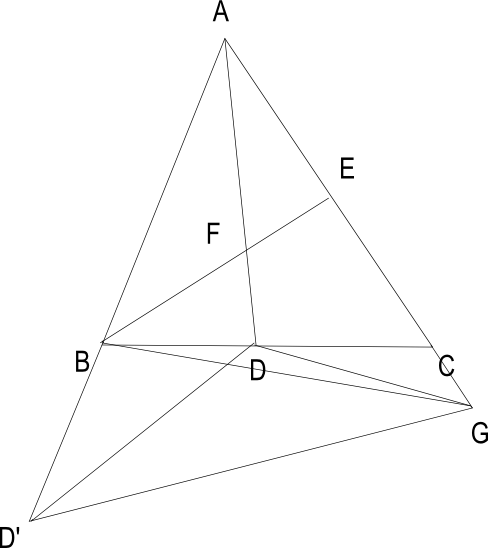
〔解答・解説〕図のように、辺 AB の延長線上に BD=BD' となる点 D'、辺 AC またはその延長線上に EB=EG となる点 G をとる。
∠ABE=∠EBC=○ とする。AG=AE+EG=AE+EB=AB+BD=AB+BD'=AD' より、三角形 AD'G は二等辺三角形である。また、BD'=BD より ∠BD'D=∠BDD'。∠BD'D+∠BDD'=∠ABC=○×2 より、∠BD'D=∠BDD'=○。三角形 ADD' と三角形 ADG において、辺 AD は共通、AD'=AG、∠DAD'=∠DAG より、2 つの三角形は合同である。よって、∠AGD=∠AD'D=○。
ここで、点 D が BG 上にないとすると、G が 辺 AC の延長線上にある場合は ∠DBG=∠EBG-∠EBD=∠EGB-∠EGD=∠DGB、また G が 辺 AC 上にある場合は ∠DBG=∠EBD-∠EBG=∠EGD-∠EGB=∠DGB となり、いずれの場合も DB=DG。これと DD'=DG より DB=DD'=BD' となるから、三角形 BDD' は正三角形である。よって、○=60°。ところが、∠A+∠B=64°+60°×2>180° であるから不適。したがって、点 D は BG 上にあることになる。
このとき、EB=EC であるから ∠C=○。∠B+∠C=○×3=180°-64°=116° より ○=116/3°。∠AFE=∠BAF+∠ABF=32°+116/3°=212/3°。ゆえに、∠DFE=180°-212/3°=328/3°。
〔寸評〕(難易度:★★★★☆)
解説における D' や G を用意するにはかなりの発想力が要求されます。さらに、D が BG 上にないことを背理法により示し、C と G が同一の点であることを導く部分はかなり難しいといえるでしょう。正解者掲示板で展開されるであろう別解が期待される問題の一つです。
A-06. シンプルなように見えて……(ぽっぽ さん)
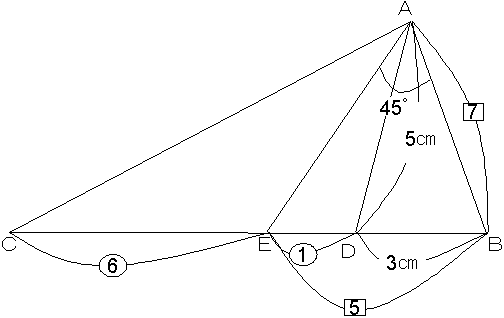
図のような三角形 ABC があります。
辺 BC 上に BD の長さが 3 cm となるように点 D をとると、AD の長さは 5 cm でした。また、辺 BC 上に 角 BAE の大きさが 45 度 となるように点 E をとると、CE:ED=6:1、EB:BA=5:7 でした。
このとき、三角形 ABC の面積は何 cm² ですか。ただし、三角形 ABE は鋭角三角形(3 つの内角がすべて 90 度より小さい三角形)とします。
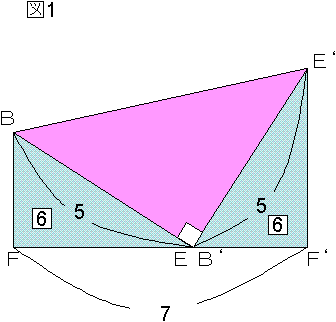
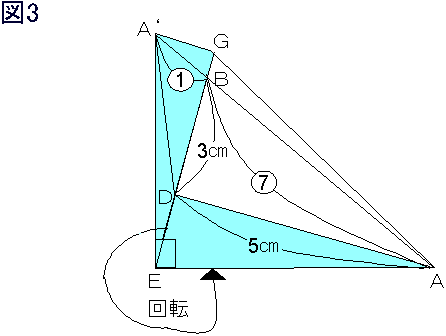
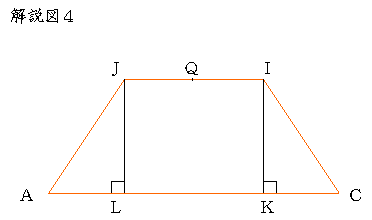
〔解答・解説〕点 E から辺 AB に下ろした垂線を EF とすると、三角形 AEF は直角二等辺三角形である。また、点 A の EF について対称な点を A' とする。
図 1 において、台形 BFF'E'=(BF+E'F')×FF'÷2=[7]×[7]÷2=[24.5]、三角形 BEE'=BE×B'E'÷2=[5]×[5]÷2=[12.5] より、三角形 BEF=([24.5]-[12.5])÷2=[6] である。よって、図 2 における真ん中の正方形の面積は [5]×[5]-[6]×4=[1] である。したがって、三角形 BEF の直角をはさむ 2 辺は足して [7]、引いて [1] であるから、BF:EF=3:4(仮に BF:EF=4:3 として三角形 ABE をかくと、∠E が直角より大きくなることがわかり、三角形 ABE が鋭角三角形であることに反する)。
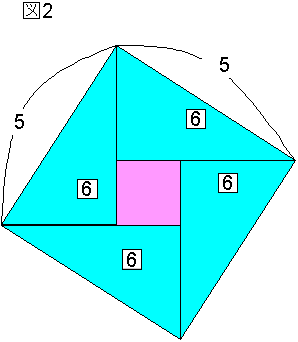
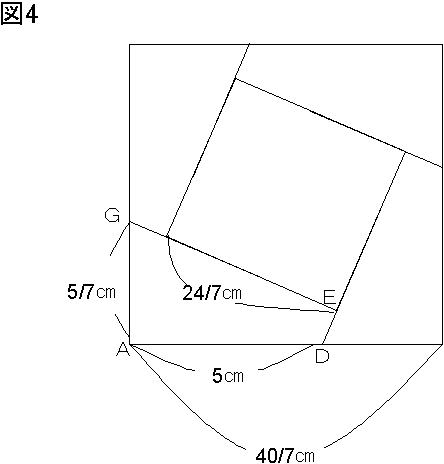
DE:CD=1:7 より 三角形 ADE=三角形 ACD×(1/7)。また、BA':BA=1:7 より 三角形 BA'D=三角形 BAD×(1/7)。よって、三角形 ADE+三角形 BA'D=(三角形 ACD+三角形 BAD)×(1/7)。ここで、A' から DA に平行な直線をひき、EB との交点を G とすると図 3 のようになり、A'G=5×(1/7)=5/7 (cm)、DG=3×(8/7)=24/7 (cm)。また、AB:AA'=7:8 より 三角形 ADE+三角形 BA'D=三角形 ADE+三角形 BGA=(四角形 A'EAD+三角形 A'AG)×(7/8)=(三角形 ADE+三角形 A'EG)×(7/8)。さらに、∠DAF=∠GA'F より ∠EA'G+∠DAE=∠EA'F+∠DAF+∠DAE=90° であるから、三角形 A'EG を点 E を中心として A' が A に重なるように回転させると、∠DEG=∠DAG=90° の四角形 ADEG ができる。
これを図 4 のように重ねると、(四角形 ADEG)×4=(40/7)×(40/7)-(24/7)×(24/7)=1024/7 (cm²) であるから、四角形 ADEG の面積は 256/49 cm²。よって、(三角形 ABC)×(8/49)=256/49 (cm²) となるので、三角形 ABC の面積は 32 cm²。
〔寸評〕(難易度:★★★★★)
辺の比が 3:4:5 の直角三角形、平行線を利用した等積変形、合同な図形を配置して求積するなど、平面幾何のさまざまな知識や手法、発想力が要求される超難問といえるでしょう。
B-07. テストの平均点(abc さん)
ある小学校で 100 人の生徒が算数のテストを受けました。
その結果、最高点が 95 点、最低点が 25 点、平均点が 38 点でした。
平均点以上の人数で考えられる最大の数を答えてください。
〔解答・解説〕100 人の合計点 38×100=3800 (点) から、最高点 95 点と最低点 25 点の 2 人の得点を除くと、3800-95-25=3680 (点)…(*)。この得点を残り 98 人に分配して、平均点以上の人ができるだけ多くなるようにすればよい。
仮に、平均点以上で最も低い点の 38 点の人が 98 人いるとすると、この 98 人の合計点は 38×98=3724 (点) となり、(*) を 3724-3680=44 (点) だけ超えてしまう。そこで、38 点を平均点より低い点で最も低い 25 点に取りかえて、取りかえる場合の数ができるだけ少なくなるようにする。44÷(38-25)=3.38… であるから 4 回取りかえる必要がある。このとき、38 点の人は 98-4=94 (人) であり、最高点の 1 人を加えて 94+1=95 (人) が平均点以上の人数で考えられる最大の数である。(得点分布の例:95点 1 人、38 点 94 人、27 点 4 人、25点 1 人)
〔寸評〕(難易度:★☆☆☆☆)
解法のポイントは極端な場合を考えることです。つるかめ算といったところでしょうか。
B-08. 正方形の移動(CRYING DOLPHIN さん)
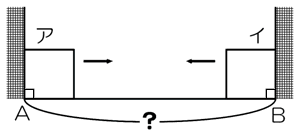
1 辺が 20 cm の 2 つの正方形ア、イが同時に出発して矢印の向きに進み、AB 上をはしからはしまで、それぞれ一定の速さですべりながら 1 往復します。(最初は図の位置、すなわちアは左はしに、イは右はしにあります)
2 つの正方形が 1 回目にぴったり重なったのは A から 50 cm の地点で、2 回目にぴったり重なったのは A から 80 cm の地点でした。
さて、A と B の間は何 cm であると考えられますか。もし答えが複数ある場合は、考えられる値をコンマ (,) で区切ってすべて答えてください。(順不同)
注 1:A と B の間は 20 cm より長いものとします。
注 2:例えば、下の図であれば「アとイは A から 25 cm の地点でぴったり重なった」ことになります。
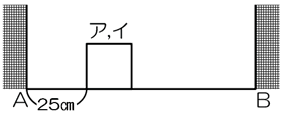
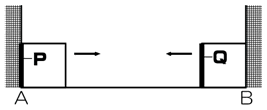
〔解答・解説〕正方形アの左端の辺を P、正方形イの左端の辺を Q とすると、正方形がぴったり重なるのは、2 つの辺 P と Q がぴったり重なるときである。そこで、2 つの辺 P と Q が往復する問題と考える。ただし、P と Q は A と「B の 20 cm 手前」の間(これを「距離 R」と表現する)を往復することに注意する。
さて、1 回目にぴったり重なるのは、P と Q が出会う(向かい合って進む)ときであるが、2 回目にぴったり重なるのは、次の 3 パターンが考えられる。
1) P と Q が出会う → P と Q の速さは同じくらい
2) P が Q に追い越される → P が Q よりも極端に遅い
3) P が Q を追い越す → P が Q よりも極端に速い
1) の場合:
出発してから P が Q と 1 回目に出会うまでに、P は 50 cm 進んでおり、P と Q が進んだ距離の和は「距離 R」1 つぶんと等しい。P と Q の 1 回目の出会いから 2 回目の出会いまでに、P と Q が進んだ距離の和は「距離 R」2 つぶんと等しい。このとき Q は 50+80=130 (cm) 進んだから、出発してから P が Q と 1 回目に出会うまでに Q が進んだ距離はこの半分で 130÷2=65 (cm)。よって、「距離 R」は 50+65=115 (cm)、AB 間は 115+20=135 (cm)。
2) の場合:
Q が 50+80=130 (cm) 進む間に、P は 80-50=30 (cm) 進む。よって、P と Q の速さの比は 30:130=3:13 である。P が 50 cm 進む間に Q は 50×13/3=650/3 (cm) 進む。したがって、「距離 R」は 50+650/3=800/3 (cm)、AB 間は 800/3+20=860/3 (cm)。
3) の場合:
P が Q を追い越す(2 回目の重なり)位置は、P と Q が出会う(1 回目の重なり)位置よりも A 寄りである。よって、条件に合わない。
以上より、答えは 135 cm と 860/3 cm である。
〔寸評〕(難易度:★★☆☆☆)
今大会で唯一の速さの問題です。2 回目に重なる場合が 3 パターンあることに注意する必要があります。数量領域の問題は 2 題とも算数らしく、解いていて楽しいですね。
B-09. 龍馬の様に斬るぜよ!(鞍馬の天狗 さん)
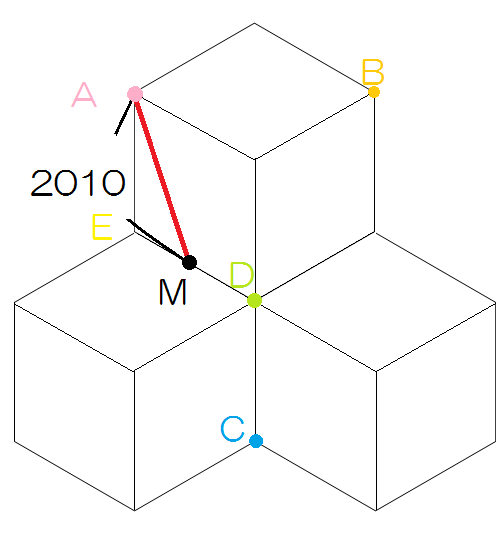
図のような同じ大きさの立方体を 4 つ重ねた立体があり、辺 DE のまん中の点を M とすると、AM の長さは 2010 cm です。
3 点 A、B、C を通る平面でこの立体を切断するとき、切り口の図形の面積は何 cm² ですか。
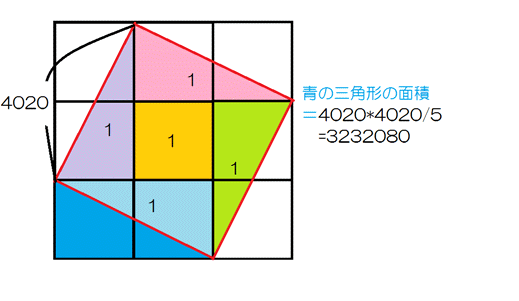
〔解答・解説〕切り口の図形は図 1 のような形(黄緑色の二等辺三角形 1 個分と緑色の台形 3 個分)になる。たて、横の長さの比が 1:2 で、AC=2010×2=4020 (cm) を対角線とする長方形 4 つと、その長方形と等しい面積の正方形 1 つを図 2 のように並べると、図 2 の左下の青色の直角三角形の面積は 4020×4020÷5=3232080 (cm²)。
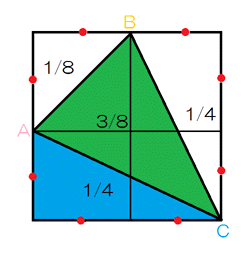
三角形 ABC は二等辺三角形で、その面積には図 3 のような関係があり、緑色の三角形の面積は青色の三角形の (3/8)÷(1/4)=3/2 (倍)。また、図 1 の台形 1 個分の面積は三角形 ABC の面積の 3/4 倍であるから、切り口の図形の面積は三角形 ABC の面積の 1+(3/4)×2=5/2 (倍)。よって、切り口の図形の面積は 3232080×(3/2)×(5/2)=12120300 (cm²)。
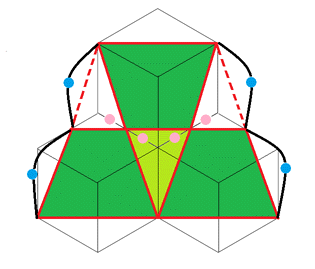
【 図 1 】
【 図 2 】
【 図 3 】
〔寸評〕(難易度:★★☆☆☆)
切り口を正しく把握することがポイントですが、二等辺三角形 ABC の面積の求め方は巧妙で面白いですね。
B-10. ジャングルジム(ゲーム10種ランキング戦 さん)
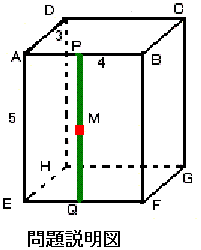
図のような AB=4 cm、AD=3 cm、AE=5 cm の直方体 ABCD-EFGH の辺のみからなる構造物と、長さ 5 cm のまっすぐな棒 PQ があります。はじめ、棒の両端 P、Q はそれぞれ辺 AB、EF 上にあります。
では、棒の両端が常に直方体の辺上にあるように棒を自由に動かすとき、棒のまん中の点 M が移動可能な部分の長さは何 cm ですか。
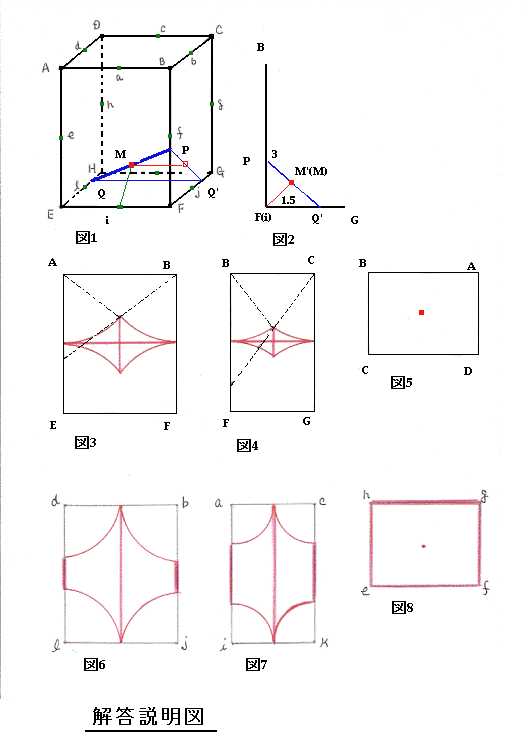
〔解答・解説〕1) P が A→B→C→D→A、Q が E→F→G→H→E と移動するとき、M は図 8 の赤色の長方形(図 3 および図 4 における赤色の横線)をえがき、その長さは (4+3)×2=14 (cm)。
2) P が A→B、Q が 辺 AE 上を E から A の方へ移動するとき、三角形 PQA は形は変化していくが常に斜辺 5 cm の直角三角形であるから、斜辺の中点 M と直角の頂点 A との距離は常に 5÷2=2.5 (cm) であり、M は半径 2.5 cm の円弧(図 3)をえがく。この動きは面 ABEF の他の頂点 B、E、F のまわりでもおこり、図 3 のような 4 つの円弧をえがく。反対側の面 CDHG でも同じ図形をえがく。
3) P が B→C、Q が 辺 BF 上を F から B の方へ移動するとき、2) と同様に 4 つの円弧(図 4)をえがく。ここで、図 3 および図 4 における各円弧の中心角を考える。図 3 の円弧 1 つと図 4 の円弧 1 つの中心角の和はちょうど直角であるから、2) と 3) の部分の長さの合計は (2.5×2)×3.14×2=31.4 (cm)。
4) 2) で 1 つめの円弧がえがかれた最終位置、すなわち P が B、Q が辺 AE 上で A からの距離が 3 cm の位置から、P が辺 BF 上を F の方へ、Q が辺 AE 上を E まで移動するとき、M は図 3 の赤色のたて線(図 7 の辺 ai 上の赤線)をえがく。
次に、Q が E→H、P が引き続き F まで移動するときを考える。Q、M から辺 FG へ下ろした垂線をそれぞれ QQ'、MM' とする(図 1、図 2)。三角形 PQ'F は形は変化していくが常に斜辺 3 cm の直角三角形であるから、斜辺の中点 M' と直角の頂点 F との距離は常に 3÷2=1.5 (cm) である。iM (=FM') の長さは常に 1.5 cm であるから、M は点 i を中心とする半径 1.5 cm、中心角 90° の円弧をえがく。
さらに、Q が H→D→A→(辺 AE 上で A からの距離が 3 cm の位置)、P が F→G→C→B と移動すると、M は図 7 の赤線(中央のたて線を除く)をえがく。この部分の長さは 2×2+(1.5×2)×3.14=13.42 (cm)。
5) 4) と同様に、P が C→G→H→D→C、Q が 辺 BF の途中から F→E→A→B→F と移動すると、M は図 6 の赤線をえがく。直線部分は 1 cm、円弧の半径は 4÷2=2 (cm) である。この部分の長さは 1×2+(2×2)×3.14=14.56 (cm)。
6) P が F→B、Q が H→D と移動するとき、M は図 6 および図 7 の中央赤色のたて線をえがく。この部分の長さは 5 cm である。
以上より、M が移動可能な部分の長さは 14+31.4+13.42+14.56+5=78.38 (cm)。
〔寸評〕(難易度:★★★★☆)
算チャレ第 699 回問題 から題材を得たとのことですが、上手くアレンジされています。M が円弧をえがき、またそれらを組み合わせることで中心角が直角になるのはとても美しいですね。通過する部分をくまなく考えるのは決してたやすくはありません。空間把握の訓練には適した問題ではないでしょうか。
B-11. いやそんなに難しくないです(君の船 さん)
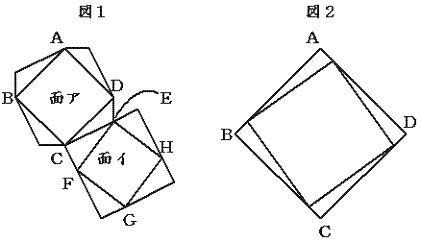
図 1 の展開図を組み立てた立体について考えます。面アは面積が 72 cm² である正方形 ABCD で、面イは面積が 48 cm² である正方形 EFGH です。
面アを底面としてこの立体を立てたとき、真上から見ると図 2 のように大きな正方形に小さな正方形が接しているように見えました。また、AC と BD の交点を P、EG と FH の交点を Q とすると、この立体において PQ の長さは 1.5 cm でした。
3 点 C、P、Q を通る平面でこの立体を切断するとき、切り口の図形のまわりの長さは何 cm ですか。
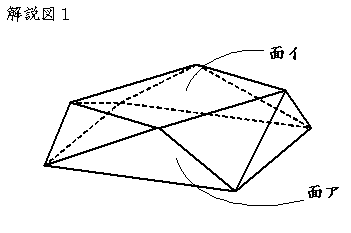
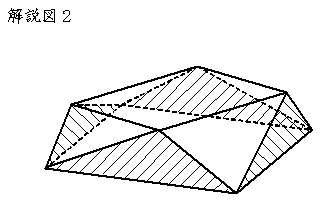
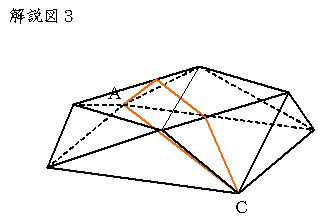
〔解答・解説〕図 1 の展開図を組み立てると、解説図 1 のような立体ができ、面アと面イは平行となる。また、真上から見ると大きな正方形に小さな正方形が接しているように見えることから、解説図 2 の斜線部分の面はすべて面アに垂直であり、互いに合同であるということがわかる。ここで、求める切り口は解説図 3 におけるオレンジ色の線である。面アの面積は 72 cm² であるから、AC×AC÷2=72 より AC=12 cm。
切断面と辺 EF、GH の交点をそれぞれ I、J とする。また、解説図 4 のように、I、J から AC に下ろした垂線をそれぞれ IK、JL とすると、(面ア):(面イ)=3:2 であるから、AL:LK:KC=1:4:1 (*) となり、AC=12 cm であることから、AL=KC=2 cm、LK=IJ=8 cm。
((*) について:問題図 2 において、正方形 ABCD の中心を O、2 つの正方形の接点のうち辺 AB、AD 上の点をそれぞれ P、Q とする。このとき、AC と PQ の交点は L である。(面ア):(面イ)=3:2 より、(三角形 APQ):(三角形 OPQ)=(1/4):(1/2)=1:2 であるから、この 2 つの三角形の底辺をともに PQ と見ると、高さの比 AL:OL も 1:2 である。図 2 は点 O に関して対称であるから、AL:LK:KC=1:(2+2):1=1:4:1 となる。)
この立体における PQ の長さ、すなわち面アを底面としたときのこの立体の高さは 1.5 cm であるから、JL=IK=1.5 cm。解説図 4 で、三角形 AJL に着目すると、∠ALJ=90°、AL=2 cm、JL=1.5 cm より、3 辺の比が 3:4:5 である直角三角形とわかる。よって、AJ=2.5 cm。三角形 CKI についても同様のことがいえて、CI=2.5 cm。
ゆえに、求める長さは JA+AC+CI+IJ=2.5+12+2.5+8=25 (cm)。
〔寸評〕(難易度:★★★★☆)
実際に組み立ててみてはいかがでしょう。展開図から立体をイメージするのは案外難しいものです。手を使わずに頭だけで考えることを想定して、難易度は高めに評価しました。
C-12. 色紙に書く条件付数値(川田 智之 さん)
赤、黄、青、白、黒の 5 色の色紙が 1 枚ずつあり、これらの色紙に互いに異なる整数を 1 つずつ書きます。
5 つの数の積が 2310 となるような色紙の組合せは何通りありますか。ただし、5 つの数の組合せが同じであっても、それらの数の書かれた色紙の組合せが異なる場合は、異なる組合せとします。
〔解答・解説〕2310 を素因数分解すると 2310=2×3×5×7×11 である。5 枚の色紙に、この 5 つの数を書く場合の数は 5×4×3×2×1=120 (通り)。また、1 枚の色紙に 1 を書く場合、5 つの素因数から 2 つを選んでそれをかけあわせた数と、他の 3 つの数を含めた 4 つの数をならべる順列の数であるから、(5×4÷2)×(5×4×3×2)=1200 (通り)。よって、求める場合の数は 120+1200=1320 (通り)。
〔寸評〕(難易度:★☆☆☆☆)
素因数分解がポイントです。5 つの数に 1 を含む場合を忘れてはいけません。
C-13. 11 月 3 日に解く問題です。(むらい さん)
A、B、C は 1 から 113 までの互いに異なる整数とします。
A+B-C=113 が成り立つような A、B、C の組合せは何通りありますか。
〔解答・解説〕C を固定して考える。
C=1 のとき A+B=114 であるから、A がとりうる値は 1~113 の 113 個考えられる。ただし、A=1 のとき A=C、A=57 のとき A=B、A=113 のとき B=C となり、条件を満たさない。よって、113-3=110 (通り)。
C=2 のとき A+B=115 であるから、A がとりうる値は 2~113 の 112 個考えられる。ただし、A=2 のとき A=C、A=113 のとき B=C となり、条件を満たさない。よって、112-2=110 (通り)。
C=3 のとき A+B=116 であるから、A がとりうる値は 3~113 の 111 個考えられる。ただし、A=3 のとき A=C、A=58 のとき A=B となり、A=113 のとき B=C となるので、条件を満たさない。よって、111-3=108 (通り)。
以下同様に、n を整数として C=n×2-1 (奇数) のときは 112-n×2 通り、C=n×2 (偶数) のときは 112-n×2 通りで、C が 111 以上では組合せは存在しない。ゆえに、求める答えは 110+110+108+108+106+106+…+4+4+2+2=(55+54+53+…+2+1)×4=6160 (通り)。
〔出題者からのコメント〕問題文の "113" を一般に "N" とすると、N が偶数のときは (N-2)²/2 通り、奇数のときは (N-1)(N-3)/2 通りとなるようです。
〔寸評〕(難易度:★★☆☆☆)
規則性を見出すことがポイントです。A、B、C のいずれか 2 数が等しくなる場合を除くことに注意する必要があります。
C-15. ある山小屋にて……(Taro さん)
Taro 君一行 40 名が山小屋に宿泊します。しかし、部屋はまったく空いていなかったので廊下に布団を敷いて泊まることになりました。
布団はたて 2 m、横 1 m で重ねて敷くことはできません。 たとえば、1 辺 2 m の正方形の部屋に布団を 2 つ敷くときは 2 通りの敷き方が考えられます。
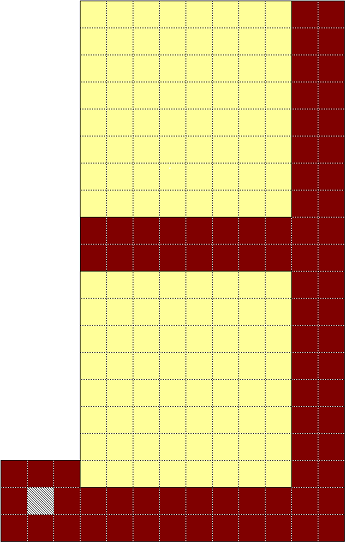
山小屋の間取りは図の通りで、黄色の部分が部屋、茶色の部分が廊下です。灰色の部分は下駄箱なので布団は敷けません。また、方眼の 1 マスは 1 m です。
では、布団の敷き方は何通り考えられますか。必要ならば 方眼 を印刷してお使いください。
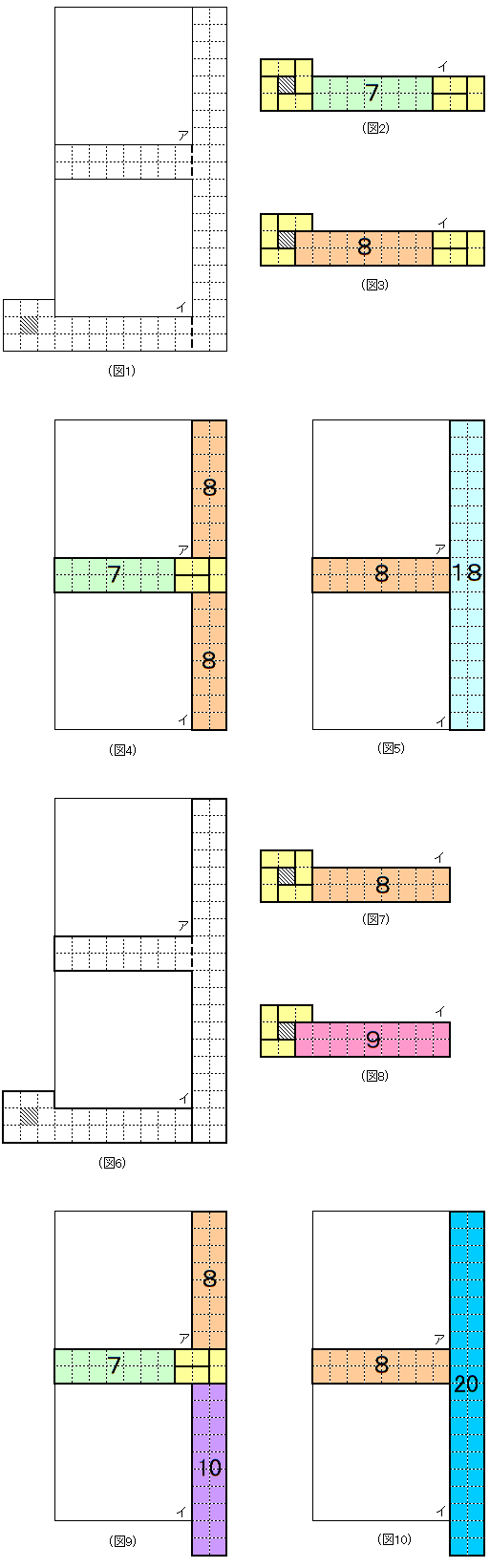
〔解答・解説〕廊下の面積と布団の数から、廊下に隙間なく布団を敷きつめなければならない。たて 2 m、横 N m の長方形に布団を N 枚敷く方法を f(N) 通りとする(N は 3 以上の整数)と、f(1)=1、f(2)=2 である。右端に布団を横に 2 枚敷くと、たて 2 m、横 (N-2) m 残るので、敷き方は f(N-2) 通り。また、右端に布団をたてに 1 枚敷くと、たて 2 m、横 (N-1) m 残るので、敷き方は f(N-1) 通り。よって、f(N)=f(N-2)+f(N-1) となり、f(3)=f(1)+f(2)=3、f(4)=f(2)+f(3)=5、… と次々と f(N) を求めていくことができ、f(7)=21、f(8)=34、f(9)=55、f(10)=89、f(18)=4181、f(20)=10946 である。
図 1 の太点線ア、イを布団がまたぐかどうかを考える。アの半分だけを布団がまたぐと仮定すると、アより左側の部分に布団を隙間なく敷きつめることはできない。よって、アの半分だけを布団がまたぐことはない。また、イの半分だけを布団がまたぐと仮定すると、右側の廊下に布団を隙間なく敷きつめることはできない。よって、イの半分だけを布団がまたぐこともない。
1) イを布団がまたぐ場合:
まず、イの右の隙間に 1 枚敷ける。下駄箱のまわりの布団の敷き方を考えて、図 2、図 3 から、イより左側の敷き方は f(7)+f(8)=55 (通り)。残りの部分の敷き方は、アをまたぐ場合(図 4)とまたがない場合(図 5)を合わせて、f(7)×f(8)×f(8)+f(8)×f(18)=166430 (通り)。よって、この場合の敷き方は 55×166430=9153650 (通り)。
2) イを布団がまたがない場合:
図 6 の太線で分けて考える。(A) と同様に考えて、図 7、図 8 から、イより左側の敷き方は f(8)+f(9)=89 (通り)。残りの部分の敷き方は、アをまたぐ場合(図 9)とまたがない場合(図 10)を合わせて、f(7)×f(8)×f(10)+f(8)×f(20)=435710 (通り)。よって、この場合の敷き方は 89×435710=38778190 (通り)。
ゆえに、すべての敷き方は 1) と 2) を合わせて 9153650+38778190=47931840 (通り)。
〔寸評〕(難易度:★★★★☆)
まっすぐな廊下に布団を敷きつめる方法の数がフィボナッチ数列をなすことを見出し、さらに廊下の形状を考慮してそれを利用するとはなかなかの難問です。
C-16. サンドイッチパーティー(ミキティ さん)
ある春の晴れた日、かのさん、あやさん、ゆうさん、さきさんの仲良し女の子 4 人組がサンドイッチパーティーをしました。
彼女たちはいくつかゲームをし、第 1 ゲームの上位から順にパン(食パン、バターロール、クロワッサン、フランスパン)、第 2 ゲームの上位から順に野菜(トマト、キュウリ、タマネギ、パプリカ)、第 3 ゲームの上位から順にトッピング (完熟ゆで卵、半熟ゆで卵、チーズ、ツナ)、第 4 ゲームの上位から順に調味料(ケチャップ、タルタルソース、マヨネーズ、マスタード)を 1 つずつ選びました。ある 1 つの食材を 2 人以上が選ぶことはしていません。
下の〈条件〉がすべて満たされるとき、4 人それぞれが食べたパン、野菜、トッピング、調味料を特定し、後の問い (1)~(4) に答えてください。
〈条件〉
- かのさんはゆで卵を食べていない。
- あやさんはクロワッサンを食べた。
- ゆうさんは赤・オレンジ・黄色と 3 色そろっているパプリカを食べた。
- さきさんはサンドイッチによく塗ってあるということでマスタードを食べた。
- フランスパンを食べた子はマヨネーズをかけたゆで卵も食べた。
- 食パンを食べた子はゆで卵を食べていない。
- ケチャップをかけた子はゆで卵も食べた。
- バターロールを食べた子はタマネギも食べたが、マスタードは食べていない。
- トマトを食べた子はさすがにケチャップを食べていない。
- 半熟ゆで卵とパプリカを一緒に食べた子はいない。
- バターロールとチーズを一緒に食べた子はいない。
(1) かのさんが食べたパンはどれですか。
a. 食パン b. バターロール c. クロワッサン d. フランスパン
(2) かのさんが食べた野菜はどれですか。
a. トマト b. キュウリ c. タマネギ d. パプリカ
(3) かのさんが食べたトッピングはどれですか。
a. 完熟ゆで卵 b. 半熟ゆで卵 c.チーズ d. ツナ
(4) かのさんが食べた調味料はどれですか。
a. ケチャップ b. タルタルソース c. マヨネーズ d. マスタード
(1)~(4) の順に、アルファベットをコンマ (,) で区切って答えてください。(例:a,b,c,d)
なお、必要ならば下の表をお使いください。
| パン | 野菜 | トッピング | 調味料 | ||||||||||||||
| 食 パ ン |
バ タ | ロ | ル |
ク ロ ワ ッ サ ン |
フ ラ ン ス パ ン |
ト マ ト |
キ ュ ウ リ |
タ マ ネ ギ |
パ プ リ カ |
完 熟 ゆ で 卵 |
半 熟 ゆ で 卵 |
チ | ズ |
ツ ナ |
ケ チ ャ ッ プ |
タ ル タ ル ソ | ス |
マ ヨ ネ | ズ |
マ ス タ | ド |
||
| 名前 | かの | ||||||||||||||||
| あや | |||||||||||||||||
| ゆう | |||||||||||||||||
| さき | |||||||||||||||||
| 調味料 | ケチャップ | ||||||||||||||||
| タルタルソース | |||||||||||||||||
| マヨネーズ | |||||||||||||||||
| マスタード | |||||||||||||||||
| ト ッピング |
完熟ゆで卵 | ||||||||||||||||
| 半熟ゆで卵 | |||||||||||||||||
| チーズ | |||||||||||||||||
| ツナ | |||||||||||||||||
| 野菜 | トマト | ||||||||||||||||
| キュウリ | |||||||||||||||||
| タマネギ | |||||||||||||||||
| パプリカ | |||||||||||||||||
〔解答・解説〕下の表において、あてはまる場所に○、あてはまらない場所に×を書いていく。
「かのはゆで卵を食べていない」ので、a に×を。
「あやはクロワッサンを食べた」ので、B に○、b に×を。
「ゆうはパプリカを食べた」ので、C に○、c に×を。
「さきはマスタードを食べた」ので、D に○、d に×を。
「フランスパンを食べた子は、マヨネーズとゆで卵を食べた」ので、E に○、e に×を。
「食パンを食べた子はゆで卵を食べていない」ので、f に×を。
「ケチャップを食べた子はゆで卵も食べた」ので、g に×を。
「バターロールを食べた子はタマネギを食べたが、マスタードは使っていない」ので、H に○、h に×を。
「トマトを食べた子はケチャップを食べていない」ので、i に×を。
「半熟ゆで卵を食べた子はパプリカを食べていない」ので、j に×を。
「バターロールを食べた子はチーズを食べていない」ので、k に×を。
| パン | 野菜 | トッピング | 調味料 | ||||||||||||||
| 食 パ ン |
バ タ | ロ | ル |
ク ロ ワ ッ サ ン |
フ ラ ン ス パ ン |
ト マ ト |
キ ュ ウ リ |
タ マ ネ ギ |
パ プ リ カ |
完 熟 ゆ で 卵 |
半 熟 ゆ で 卵 |
チ | ズ |
ツ ナ |
ケ チ ャ ッ プ |
タ ル タ ル ソ | ス |
マ ヨ ネ | ズ |
マ ス タ | ド |
||
| 名前 | かの | b | c | a | a | d | |||||||||||
| あや | b | b | B | b | c | d | |||||||||||
| ゆう | b | c | c | c | C | d | |||||||||||
| さき | b | c | d | d | d | D | |||||||||||
| 調味料 | ケチャップ | e | i | g | g | ||||||||||||
| タルタルソース | e | ||||||||||||||||
| マヨネーズ | e | e | e | E | e | e | |||||||||||
| マスタード | h | e | h | ||||||||||||||
| ト ッピング |
完熟ゆで卵 | f | |||||||||||||||
| 半熟ゆで卵 | f | j | |||||||||||||||
| チーズ | k | e | |||||||||||||||
| ツナ | e | ||||||||||||||||
| 野菜 | トマト | h | |||||||||||||||
| キュウリ | h | ||||||||||||||||
| タマネギ | h | H | h | h | |||||||||||||
| パプリカ | h | ||||||||||||||||
さきはマスタードを食べたが、クロワッサンは食べていないので、「クロワッサンは食べた子はマスタードを食べていない」ことが分かる。よって、「食パンを食べた子はマスタードを食べ」、「その子はさきである」ことも分かる。(L に○、l に×)
| パン | 野菜 | トッピング | 調味料 | ||||||||||||||
| 食 パ ン |
バ タ | ロ | ル |
ク ロ ワ ッ サ ン |
フ ラ ン ス パ ン |
ト マ ト |
キ ュ ウ リ |
タ マ ネ ギ |
パ プ リ カ |
完 熟 ゆ で 卵 |
半 熟 ゆ で 卵 |
チ | ズ |
ツ ナ |
ケ チ ャ ッ プ |
タ ル タ ル ソ | ス |
マ ヨ ネ | ズ |
マ ス タ | ド |
||
| 名前 | かの | l | × | × | × | × | × | ||||||||||
| あや | × | × | ○ | × | × | × | |||||||||||
| ゆう | l | × | × | × | × | ○ | × | ||||||||||
| さき | L | l | × | l | × | × | × | × | ○ | ||||||||
| 調味料 | ケチャップ | l | × | × | × | × | |||||||||||
| タルタルソース | l | × | |||||||||||||||
| マヨネーズ | × | × | × | ○ | × | × | |||||||||||
| マスタード | L | × | l | × | × | ||||||||||||
| ト ッピング |
完熟ゆで卵 | × | |||||||||||||||
| 半熟ゆで卵 | × | × | |||||||||||||||
| チーズ | × | × | |||||||||||||||
| ツナ | × | ||||||||||||||||
| 野菜 | トマト | × | |||||||||||||||
| キュウリ | × | ||||||||||||||||
| タマネギ | × | ○ | × | × | |||||||||||||
| パプリカ | × | ||||||||||||||||
表を見ながら同様に、バターロールを食べた子はタマネギを食べているので、「パプリカを食べたゆうはバターロールを食べていない」ことが分かる。よって、「かのはバターロールを食べ」、「ゆうはフランスパンを食べた」ことも分かる。(M に○、m に×)
そこから、「ゆうはマヨネーズを食べた」ことも分かる。(N に○、n に×)
| パン | 野菜 | トッピング | 調味料 | ||||||||||||||
| 食 パ ン |
バ タ | ロ | ル |
ク ロ ワ ッ サ ン |
フ ラ ン ス パ ン |
ト マ ト |
キ ュ ウ リ |
タ マ ネ ギ |
パ プ リ カ |
完 熟 ゆ で 卵 |
半 熟 ゆ で 卵 |
チ | ズ |
ツ ナ |
ケ チ ャ ッ プ |
タ ル タ ル ソ | ス |
マ ヨ ネ | ズ |
マ ス タ | ド |
||
| 名前 | かの | × | M | × | m | × | × | × | n | × | |||||||
| あや | × | × | ○ | × | × | n | × | ||||||||||
| ゆう | × | m | × | M | × | × | × | ○ | n | n | n | n | N | × | |||
| さき | ○ | × | × | × | × | × | × | × | ○ | ||||||||
| 調味料 | ケチャップ | × | × | × | n | × | × | ||||||||||
| タルタルソース | × | × | n | ||||||||||||||
| マヨネーズ | × | × | × | ○ | n | n | n | N | × | × | |||||||
| マスタード | ○ | × | × | × | × | n | |||||||||||
| ト ッピング |
完熟ゆで卵 | × | |||||||||||||||
| 半熟ゆで卵 | × | × | |||||||||||||||
| チーズ | × | × | n | ||||||||||||||
| ツナ | × | n | |||||||||||||||
| 野菜 | トマト | × | n | ||||||||||||||
| キュウリ | × | n | |||||||||||||||
| タマネギ | × | ○ | × | × | |||||||||||||
| パプリカ | n | × | n | N | |||||||||||||
次に、「完熟ゆで卵を食べた子はパプリカを食べ」、「フランスパンを食べた子は完熟ゆで卵を食べた」ことも分かる。(P に○、p に×)
ここで、もし、かのがケチャップを食べたとすると、ケチャップを食べた子はゆで卵を食べているので、今までの内容に矛盾する。よって、「かのはタルタルソースを食べ」、「バターロールを食べた子はタルタルソースを食べた」ことも分かる。(Q に○、q に×)
| パン | 野菜 | トッピング | 調味料 | ||||||||||||||
| 食 パ ン |
バ タ | ロ | ル |
ク ロ ワ ッ サ ン |
フ ラ ン ス パ ン |
ト マ ト |
キ ュ ウ リ |
タ マ ネ ギ |
パ プ リ カ |
完 熟 ゆ で 卵 |
半 熟 ゆ で 卵 |
チ | ズ |
ツ ナ |
ケ チ ャ ッ プ |
タ ル タ ル ソ | ス |
マ ヨ ネ | ズ |
マ ス タ | ド |
||
| 名前 | かの | × | ○ | × | × | × | × | × | q | Q | × | × | |||||
| あや | × | × | ○ | × | × | Q | q | × | × | ||||||||
| ゆう | × | × | × | ○ | × | × | × | ○ | × | × | × | × | ○ | × | |||
| さき | ○ | × | × | × | × | × | × | × | ○ | ||||||||
| 調味料 | ケチャップ | × | q | Q | × | × | × | × | × | ||||||||
| タルタルソース | × | Q | q | × | × | ||||||||||||
| マヨネーズ | × | × | × | ○ | × | × | × | ○ | × | × | |||||||
| マスタード | ○ | × | × | × | × | × | |||||||||||
| ト ッピング |
完熟ゆで卵 | × | p | p | P | p | p | p | P | ||||||||
| 半熟ゆで卵 | × | p | × | ||||||||||||||
| チーズ | × | × | × | ||||||||||||||
| ツナ | × | × | |||||||||||||||
| 野菜 | トマト | × | × | ||||||||||||||
| キュウリ | × | × | |||||||||||||||
| タマネギ | × | ○ | × | × | |||||||||||||
| パプリカ | × | × | × | ○ | |||||||||||||
よって、最終的には次のようになる。(ある程度埋まれば、あとはスイスイ進められることだろう。)
| パン | 野菜 | トッピング | 調味料 | ||||||||||||||
| 食 パ ン |
バ タ | ロ | ル |
ク ロ ワ ッ サ ン |
フ ラ ン ス パ ン |
ト マ ト |
キ ュ ウ リ |
タ マ ネ ギ |
パ プ リ カ |
完 熟 ゆ で 卵 |
半 熟 ゆ で 卵 |
チ | ズ |
ツ ナ |
ケ チ ャ ッ プ |
タ ル タ ル ソ | ス |
マ ヨ ネ | ズ |
マ ス タ | ド |
||
| 名前 | かの | × | ○ | × | × | × | × | ○ | × | × | × | × | ○ | × | ○ | × | × |
| あや | × | × | ○ | × | × | ○ | × | × | × | ○ | × | × | ○ | × | × | × | |
| ゆう | × | × | × | ○ | × | × | × | ○ | ○ | × | × | × | × | × | ○ | × | |
| さき | ○ | × | × | × | ○ | × | × | × | × | × | ○ | × | × | × | × | ○ | |
| 調味料 | ケチャップ | × | × | ○ | × | × | ○ | × | × | × | ○ | × | × | ||||
| タルタルソース | × | ○ | × | × | × | × | ○ | × | × | × | × | ○ | |||||
| マヨネーズ | × | × | × | ○ | × | × | × | ○ | ○ | × | × | × | |||||
| マスタード | ○ | × | × | × | ○ | × | × | × | × | × | ○ | × | |||||
| ト ッピング |
完熟ゆで卵 | × | × | × | ○ | × | × | × | ○ | ||||||||
| 半熟ゆで卵 | × | × | ○ | × | × | ○ | × | × | |||||||||
| チーズ | ○ | × | × | × | ○ | × | × | × | |||||||||
| ツナ | × | ○ | × | × | × | × | ○ | × | |||||||||
| 野菜 | トマト | ○ | × | × | × | ||||||||||||
| キュウリ | × | × | ○ | × | |||||||||||||
| タマネギ | × | ○ | × | × | |||||||||||||
| パプリカ | × | × | × | ○ | |||||||||||||
以上より
- かの ‐ バターロール ‐ タマネギ ‐ ツナ ‐ タルタルソース
- あや ‐ クロワッサン ‐ キュウリ ‐ 半熟ゆで卵 ‐ ケチャップ
- ゆう ‐ フランスパン ‐ パプリカ ‐ 完熟ゆで卵 ‐ マヨネーズ
- さき ‐ 食パン ‐ トマト ‐ チーズ ‐ マスタード
となるから、答えは b,c,d,b である。
〔出題者からのコメント〕
数独(ナンバープレイス)は自動解答ソフトが豊富、カックロ(サムクロス)は画像作成が面倒、ぬりかべはパズルそのものができても、良い設問が思いつかないとの理由で、今回は過去に出したことがある推理パズルになってしまいました。
しかし、問題はオリジナルです。ただ、元ネタはちゃんとございまして、「S/mileage DVD MAGAZINE vol.1」という女性アイドル DVD のサンドイッチパーティーを参考にしています。
ただし、
- 名前(福田花音=かのん、和田彩花、前田憂佳=ゆうか、小川紗季)がそのままだと知っている人にはバレバレなので、頭 2 文字のみをとり、
- 4 品だとやや複雑になると思ったので、メインディッシュの肉料理 1 品を省きました。なので、ややベジタリアンな女の子という設定に変えられています。(^^;;
推理パズルにありがちな「数値の優劣」が出てこないので、難度はかなり低いと思います。解くのには印刷をしないと少々面倒かもしれませんが。
○ 検索キーワード
推理パズル http://www.nikoli.co.jp/ja/puzzles/suiri_puzzle/
マトリックス
三段論法
スマイレージ (S/mileage)
DVD MAGAZINE
サンドイッチ頂上決戦
〔寸評〕(難易度:★★☆☆☆)
ミキティさんおなじみの推理パズルです。注意点としては、ゆで卵に「完熟」と「半熟」があることでしょうか。問題の背景にはなかなか奥深いものがありますね。
