A-01. 怪しい平面図形(君の船 さん)
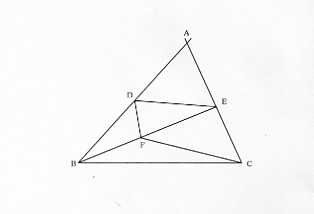
図のような三角形 ABC があります。辺 AB、AC 上にそれぞれ点 D、E をとり、BE 上に点 F をとりました。そして、C と F、D と F を結んだところ、角 ACF=52.5 度、角 AED=65 度、角 BED=30 度、角 BCF=17.5 度、角 DBE=25 度 でした。
このとき、角 BDF は何度ですか。
〔解答・解説〕∠CEB=180°-(65°+30°)=85° より、∠CFE=180°-(52.5°+85°)=42.5°。
よって、∠CBE=42.5°-17.5°=25°=∠ABE。
したがって、三角形 BDE を、BE を軸として折り返し、三角形 BD'E をつくると、頂点 D' は辺 BC 上にあることがわかる。
D' と E、F を結ぶと、∠CED'=85°-30°=55°、∠CD'E=180°-(52.5°+17.5°+55°)=55° であるから、CD'=CE。
ここで、BE 上に∠ECG=10°となるような点 G をとると、∠CGE=180°-(85°+10°)=85°=∠CEG であるから、CG=CE=CD'。
これと、∠D'CG=(52.5°+17.5°)-10°=60° であることから、三角形 CD'G は正三角形である。
∠GCF=52.5°-10°=42.5°=∠GFC より、FG=CG=D'G。
これと、∠D'GF=180°-(85°+60°)=35° であることから、∠FD'G=(180°-35°)÷2=72.5°。
よって、∠FD'C=60°+72.5°=132.5°。
したがって、∠BDF=∠FD'B=180°-132.5°=47.5°。
A-02. ∠ ななめ 45°(長野 美光 さん)
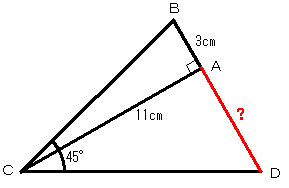
図の三角形 BCD は角 BCD が 45 度の鋭角三角形(3 つの内角がすべて 90 度より小さい三角形)です。頂点 C から 辺 BD に垂線 CA を下ろしたところ、AB=3 cm、AC=11 cm でした。
このとき、AD の長さは何 cm ですか。
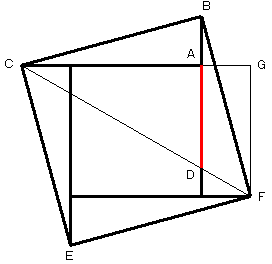
〔解答・解説〕図のように、三角形 ABC を 4 つ組み合わせて正方形 BCEF をつくると、対角線 CF と辺 AB の延長線との交点が D となる。
三角形 CFG において、CG=11+3=14 (cm)、FG=11-3=8 (cm)。
三角形 CDA と 三角形 CFG は相似であるから、AD=AC×(8/14)=44/7 (cm)。
別解(三角関数利用):
tan∠BCD=1、tan∠ACB=3/11 であるから、tan の加法定理 tan∠BCD=(tan∠ACB+tan∠ACD)/(1-tan∠ACB tan∠ACD) より、tan∠ACD=4/7。
ゆえに、AD=AC×(4/7)=44/7 (cm)。
A-03. 図形の問題です。(むらい さん)
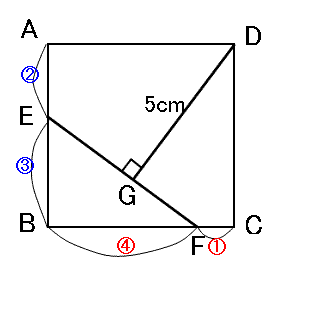
正方形 ABCD において、辺 AB を 2:3 に分ける点を E、辺 BC を 4:1 に分ける点を F とし、E と F を結びます。頂点 D から EF に垂線 DG を下ろしたところ、DG=5 cm でした。
このとき、正方形 ABCD の 1 辺の長さは何 cm ですか。
〔解答・解説〕正方形の 1 辺の長さを 5×a cm とすると、EF の長さは 5×a cm。
D と E、F を結ぶと、三角形 EBF=6×a×a cm²、三角形 AED=5×a×a cm²、三角形 DFC=(5/2)×a×a cm²。
よって、三角形 DEF=(23/2)×a×a cm²。
したがって、DG=(23/5)×a=5 (cm) であるから、a=25/23。
ゆえに、正方形の 1 辺の長さは 5×(25/23)=125/23 (cm)。
A-04. 4 つの四分円(だいすけ さん)
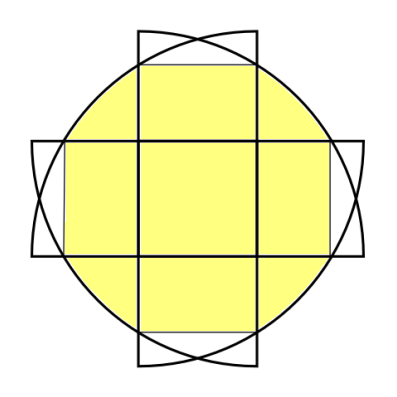
図のように、半径 6 cm の四分円(中心角が 90 度のおうぎ形)を、中央に 1 辺 3 cm の正方形ができるように 4 個重ねました。
このとき、黄色の部分の面積は何 cm² ですか。
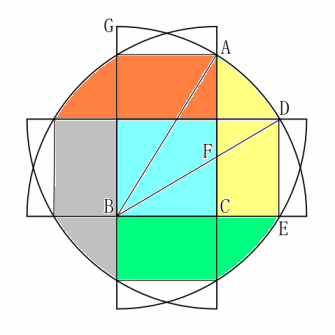
〔解答・解説〕図のように分割する。
まず、黄色の図形 ACED の面積を求める。
AB=BD=6 cm、BC=DE=3 cm、∠ACB=∠BED=90° であるから、三角形 ABC と三角形 BDE は合同で面積は等しい。
共通部分の三角形 BCF を除いた、三角形 ABF と四角形 CEDF の面積も等しい。
よって、黄色の図形 ACED とおうぎ形 ABD の面積は等しい。
また、BD=6 cm、DE=3 cm より、∠DBE=30°。
同様に、∠ABG=30°。
したがって、∠ABD=90°-(30°+30°)=30°。
よって、黄色の図形 ACED の面積は 6×6×3.14×(30/360)=9.42 (cm²)。
緑色、灰色、オレンジ色の部分の面積も同じく 9.42 cm²。
また、中央の水色の正方形の面積は 3×3=9 (cm²)。
ゆえに、求める面積は 9.42×4+9=46.68 (cm²)。
A-05. 三角形の面積(英ちゃん さん)
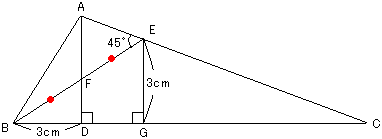
図のような三角形 ABC があります。頂点 A から辺 BC に垂線 AD を下ろしたところ、BD=3 cm でした。また、角 AEB が 45 度となるように、辺 AC 上に点 E をとり、AD と BE の交点を F とすると、BF=FE でした。さらに、E から辺 BC に垂線 EG を下ろしたところ、EG=3 cm でした。
このとき、三角形 ABC の面積は何 cm² ですか。
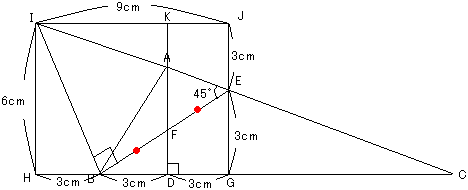
〔解答・解説〕図のように、長方形 GHIJ をつくる。
長方形 GHIJ=6×9=54 (cm²)、三角形 BGE=6×3÷2=9 (cm²)、三角形 IHB=6×3÷2=9 (cm²)、三角形 IJE=9×3÷2=13.5 (cm²)。
よって、三角形 BIE の面積は 54-(9+9+13.5)=22.5 (cm²)。
また、IA:AE:EC=2:1:3 であるから、IE:AC=3:4。
したがって、三角形 ABC の面積は 22.5×(4/3)=30 (cm²)。
A-06. 三角形の面積は?(ごんごんま さん)
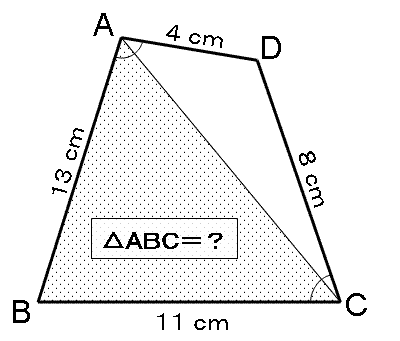
図のような、AB=13 cm、BC=11 cm、CD=8 cm、DA=4 cm の四角形 ABCD があります。
角 BAD=角 BCD のとき、三角形 ABC の面積は何 cm² ですか。
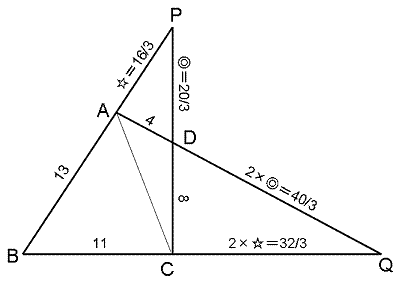
〔解答・解説〕図のように、辺 AB と辺 CD の延長線との交点を P、辺 AD と辺 BC の延長線との交点を Q とする。
∠PAD=∠QCD(∠BAD=∠BCD より)、∠PDA=∠QDC(対頂角)、AD:CD=4:8=1:2 であるから、三角形 PAD と三角形 QCD は相似で、辺の長さの比は 1:2 である。
よって、PA:QC=PD:QD=1:2。
したがって、PA=☆ cm、PD=◎ cm とおくと、QC=2×☆ cm、QD=2×◎ cm。
∠B は共通、∠BAD=∠BCD、AB:BC=13:11 であるから、三角形 PBC と三角形 QBA は相似で、辺の長さの比は 11:13 である。
よって、PB:QB=PC:QA=11:13。
したがって、13×PB=11×QB、13×PC=11×QA。
一方、PB=(13+☆) cm、QB=(11+2×☆) cm、PC=(8+◎) cm、QA=(4+2×◎) cm であるから、13×(13+☆)=11×(11+2×☆)、13×(8+◎)=11×(4+2×◎)。
これを解いて、☆=16/3、◎=20/3。
よって、三角形 PAD は辺の長さの比が AD:PA:PD=3:4:5 の直角三角形であり、その面積は 4×(16/3)÷2=32/3 (cm²)。
また、PD:DC=(20/3):8=5:6 より、(三角形 PAC):(三角形PAD)=PC:PD=(5+6):5=11:5。
したがって、三角形 PAC の面積は (32/3)×(11/5)=352/15 (cm²)。
(三角形 ABC):(三角形 PAC) =AB:AP=13:(16/3)=39:16 であるから、三角形 ABC の面積は (352/15)×(39/16)=57.2 (cm²)。
A-07. やっぱり図形問題が好き(CRYING DOLPHIN さん)
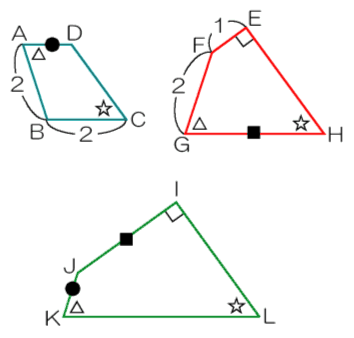
3 つの四角形 ABCD、EFGH、IJKL があります。
- 辺 AD と辺 BC は平行
- AB=BC=FG=2 cm、EF=1 cm
- AD=JK、GH=IJ
- 角 A=角 G=角 K=72 度、角 C=角 H=角 L=54 度
- 角 E と角 I は直角
以上のことが成り立っています。
このとき、面積比 (四角形 ABCD):(四角形 EFGH):(四角形 IJKL) を、最も簡単な整数比で表してください。
〔解答・解説〕∠F=∠J=144°、∠A=∠G=∠K=72° あたりから、(1 つの内角が 144°、1 辺 2 cm の)正十角形に埋め込むことを考える。
左上図のように、正十角形を合同な 10 個の二等辺三角形に分割し、二等辺三角形の 1 つを P とする。
- 四角形 ABCD について:
右上図のように、P 1 個に変形できる。 - 四角形 EFGH について:
左下図のように 2 つくっつければ P 3 個分になる。
すなわち、四角形 EFGH は P 1.5 個分。 - 四角形 IJKL について:
これがちょっと(かなり?)くせもので、右下図のようになる。
正十角形の中心を M とすると、MJ=MK=NI=NL、∠JMK+∠INL=36°+144°=180° であるから、三角形 JKM と三角形 ILN の面積は等しく(※)、三角形 JKM を三角形 ILN に等積移動することができる。よって、四角形 IJKL の面積は P 3 個分とわかる。
以上より、求める面積比は 1:1.5:3=2:3:6
〔出題者からのコメント〕(※)の部分の厳密な証明はかなり面倒です。
後日解説の完全版を提出するかも。。
(今日は解説完全版を書く気力がありません orz)
正十角形に図形を埋め込む構想自体は数年前からあったのですが、難問過ぎるかも。。汗
A-08. 正十二角形を折る(なか さん)
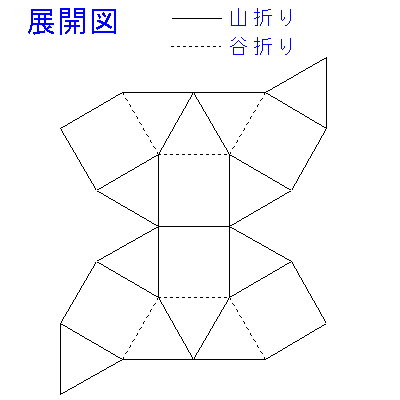
正十二角形を二分し、それらを背中合わせにつないで、図のような展開図を作りました。すべての面は正方形または正三角形で、1 つの正方形の面積は 32 cm² です。
これを組み立ててできる立体の体積は何 cm³ ですか。
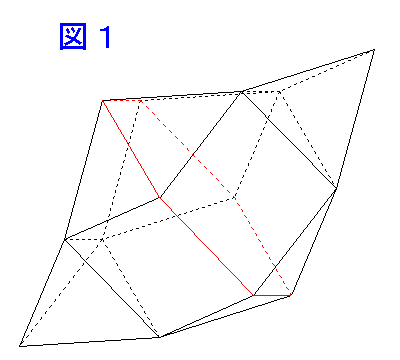
〔解答・解説〕できる立体は図 1 のとおりで、もともと正十二角形の辺であったところがこの立体では正六角形になっている(図の赤線)。
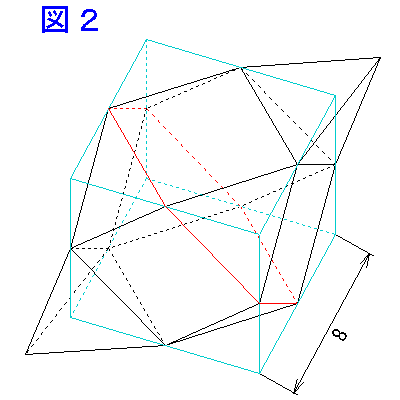
この六角形に沿って立体をいったん切り離し、60° ひねってつなぎ直すと、図 2 のように、正方形の 6 つの面が 1 辺 8 cm の立方体にぴったりはまる。
もちろん、ひねったからといって体積は変わらないので、図 2 の立体の体積を求めればよい。
- 正四面体 2 個(とがった部分):
1 辺 4 cm の立方体の頂点を結ぶ正四面体であるから、
1 個分の体積は 4×4×4÷3=64/3 (cm³)。 - 残る 14 面体(芯の部分):
1 辺 8 cm の立方体の 8 隅を切り落とした形であるから、
体積は 8×8×8-4×4×4÷6×8=(512-256/3) (cm³)。
よって、求める体積は (64/3)×2+(512-256/3)=1408/3 (cm³)。
B-09. 分数→整数(ヤマラー さん)
3 つの分数 104/153、143/255、364/459 のいずれにかけても整数になるような分数のうち、最も小さいものを求めてください。
〔解答・解説〕求める分数の分子は、3 つの分数の分母 153、255、459 の最小公倍数であるから、2295。
また、求める分数の分母は、3 つの分数の分子 104、143、364 の最大公約数であるから、13。
よって、求める分数は 2295/13。
B-10. 水槽(数学爺 さん)
甲、乙 2 つの水槽があり、容積の比は 3:2 です。また、2 つの水道管 A、B があり、A で甲の水槽、B で乙の水槽に給水すると、満水になるまでの時間の比は 2:3 です。
では、A で乙の水槽、B で甲の水槽に給水する場合、同時に満水にするためには、甲の水槽にどれだけ水が溜まったとき、乙の水槽に給水を始めるとよいですか。満水時を 1 として、分数で答えてください。
〔解答・解説〕甲、乙の水槽の容積をそれぞれ 3、2 とし、A で甲の水槽、B で乙の水槽に給水したとき、それぞれの水槽が満水になるまでの時間を 2、3 とする。
A、B で給水できる量はそれぞれ 1 時間あたり 3/2、2/3 であるから、A で乙の水槽を満水にするのにかかる時間は 2÷(3/2)=4/3 (時間)、B で甲の水槽を満水にするのにかかる時間は 3÷(2/3)=9/2 (時間) である。
よって、A で乙の水槽に給水するよりも、9/2-4/3=19/6 (時間) だけ早く、B で甲の水槽に給水を始めればよい。
B で甲の水槽を満水にするのに 9/2 時間かかるから、答えは (19/6)÷(9/2)=19/27。
B-11. たまたま(?)です(ぶぶおパパ さん)
G さんの家から温泉までの道のりは、平地だけでなく上り坂や下り坂があります。
あるとき、G さんが家と温泉の間を往復するのに、上り坂では分速 30 m、下り坂では分速 45 m、平地では分速 36 m で休まず歩いたところ、家から温泉までは 2 時間 12 分、温泉から家までは 2 時間 33 分かかりました。
では、家から温泉までの道のりのうち、平地の長さは何 m よりも短いといえますか。
〔解答・解説〕2÷(1/30+1/45)=36 より、分速 30 m と分速 45 m の平均の速さは分速 36 m で、これが平地での速さとたまたま一致していることがこの問題のポイント。
行きに「上り」だった道は帰りでは「下り」になり、行きに「下り」だった道は帰りでは「上り」になるため、往復での「上りの道のりの合計」と「下りの道のりの合計」は等しい。
よって、上りと下りで進む速さを平均して考えることができ、それが平地の速さ (分速 36 m) に等しいから、往復するのにかかる時間は「すべての道のりが平地だった場合」と等しいことになる。
2 時間 12 分+2 時間 33 分=285 分であるから、家から温泉までの道のりは 36×285÷2=5130 (m)。
また、行きと帰りのかかった時間の差は 21 分であり、1 m 進むのに「上り」と「下り」では 1/30-1/45=1/90 (分) の差ができるので、行きは「上り」よりも「下り」の方が 21÷1/90=1890 (m) 長いことがわかる。
ゆえに、家から温泉までの道のりのうち平地の長さは 5130-1890=3240 (m) よりも短いといえる。
B-12. 流水算(ヒデー王子 さん)
ある川の上流の A 地点と B 地点の間を、甲、乙の両船が何度も往復しています。
ある日、甲は A 地点を、乙は B 地点を共に 8 時ちょうどに出発し、互いに一度も追い越されることなく、5 回すれ違った後、甲は 2 往復半、乙は 3 往復して B 地点に 11 時 18 分に同時に到着しました。甲、乙の静水時の速さ、川の流速はそれぞれ一定であり、甲の下りの速さと乙の上りの速さが等しく、両船が最後にすれ違ったところは A 地点から 0.5 km 下ったところでした。
では、この川の流速は時速 何 km ですか。
〔解答・解説〕AB 間を甲が下る時間(=乙が上る時間)を □、甲が上る時間を P、乙を下る時間を Q とすると、□×3+P×2=□×3+Q×3 より、P×2=Q×3。
よって、P:Q=3:2。
したがって、甲が上る速さを <2> とすると、乙が下る速さは <3>。
ここで、甲が下る速さと乙が上る速さは等しいから、甲が下る速さ(乙が下る速さ)は (<2>+<3>)÷2=<2.5>、川の流速は (<3>-<2.5>)÷2=<0.25>。
よって、時間の比は □:P:Q=(1/2.5):(1/2):(1/3)=12:15:10 となり、次のダイヤグラムを得る。
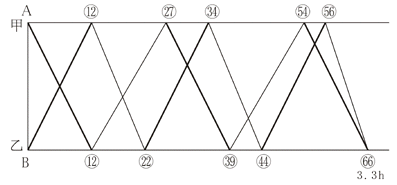
AB 間を甲が下る時間(乙が上る時間)は 3.3×(12/66)=0.6 (時間)、AB 間の距離は 0.5×{(12×2)/(56-54)}=6 (km) であるから、甲が下る速さ(乙が上る速さ)は 6÷0.6=10 (km/時)。
ゆえに、川の流速は 10×(0.25/2.5)=1 (km/時)。
B-13. Prime Railways(sugitakukun さん)
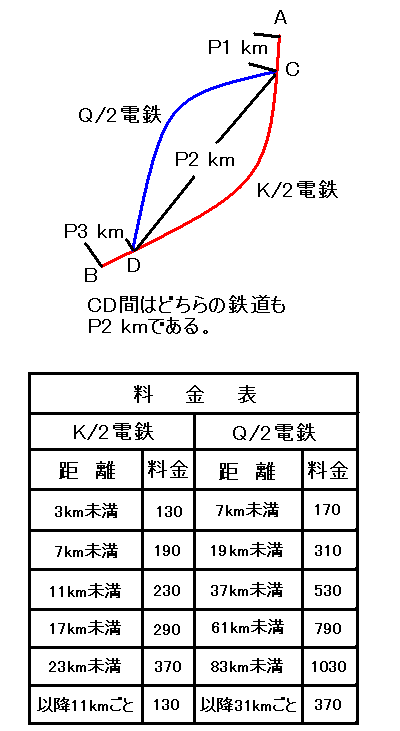
上の図のような 2 本の鉄道が敷かれている地方があります。2 つの鉄道はそれぞれ 1 km ごとに駅が設置されており、主要駅間距離である図中の P1、P2、P3 はいずれも 2 桁以上の素数です。また、K/2 電鉄の総延長距離である P1+P2+P3 は 200 を超える最小の素数であり、Q/2 電鉄の総延長距離 P2 は、以上の条件を満たす P2 のうち、最大のものです。
ある人が C 駅から D 駅まで、「駅間はすべて鉄道を利用し(注)、かつ所要金額が最も安くなるように」移動したところ、C 駅出発時の所持金が 100×素数(円)だったのに対し、D 駅到着時の所持金は 10×素数(円)になっていました。
このとき、この人の D 駅到着時の所持金として考えられる最小の金額は何円ですか。
注:次の駅まで 1 駅歩くといったことはせず、鉄道で合計 P2 km を移動するという意味です。
〔解答・解説〕まず、P2 を求める。
P1+P2+P3 は 200 を超える最小の素数であるから 211。
P1、P3 はそれぞれ 11 以上であるから、P2 は 189 以下。
189 以下の最大の素数は 181 であるが、(P1,P2,P3) の組として、(11,181,19)、(13,181,17) が存在するので、P2 は 181 である。
さて、181 km をそれぞれの鉄道を使って移動することを考える。
K/2 電鉄の場合、23+11×14<181<23+11×15 であるから、料金は 370+130×15=2320 (円)。
Q/2 電鉄の場合、83+31×3<181<83+31×4 であるから、料金は 1030+370×4=2510 (円)。
よって、最安値は 2320 円……と思いがちであるが、この金額は「到着時の所持金が素数×10 円」を満たしていない。
そこで、「Q/2 電鉄の料金の変わり目が 176 km であること」と「遠距離での Q/2 電鉄の料金の上がり幅が初乗り料金より高いこと」に注意すると、「料金が上がる直前で途中下車し、上がり幅より安い切符で再乗車する」ことに気づくだろう。
「175 km で一旦途中下車し、残り 6 kmを 170 円で再乗車する」と、Q/2 電鉄の料金が (1030+370×3)+170=2310 (円) となり、K/2 電鉄の料金を下回るので、Q/2 電鉄のほうが料金が安くなることがわかる。
次に、2300 円以下にできるかどうかを調べる。
[a] 100 円で進める距離から考える:
181 km を 2300 円で進むためには、100 円当たり 181/23=7.86… (km) 進まなければならないが、61 km 未満の料金区分ではどのようにしても 100 円当たり 7.86 km は進めない(最大 790 円で 60 km → 100 円当たり 7.59 km)。
よって、61 km 未満の距離をどのように組み合わせても、181 km を 2300 円以下で進むことはできないので、1030 円以上払う区間が存在することになる。
[b] 長い区間から考える:
1030 円以上払う区間を I とし、この区間がどの料金区分かにより場合分けする。ここで、できるだけ安くするために、区間 I は料金区分の最大距離としてよい。すなわち、
1) 区間 I が 175 km(2140 円)→ 残り 6 km を 160 円以内
2) 区間 I が 144 km(1770 円)→ 残り 37 km を 530 円以内
3) 区間 I が 113 km(1400 円)→ 残り 68 km を 900 円以内
4) 区間 I が 82 km(1030 円)→ 残り 99 km を 1270 円以内
の 4 パターンに分けられるが、残り 6 km を 160 円以内で進むことはできないから、1) は不適。
2) について:
36 km なら 530 円であるが、37 km はギリギリで届かない。
37 km を分割するにも、530 円以下に抑える方法が 170×3 円 (18km) または 310+170 円 (24 km) のみであるから不適。
3) について:
68 km 通して乗るのは 1030 円で不適。
60 km 未満の区分で分割しても、残り 110 円しかないので不適。
36 km を 530 円で乗っても、残り 32 km を 370 円で進むことはできないので不適。
それ以下は、単純な足し算でも届かないので不適。
4) について:
再び [a] の考え方を用いると、99÷12.7=7.79… であるから、残りの 99 km についても 1030 円以上払う区間 J が必要になる。
ところが、残り 1270 円しかないので、区間 J は 82 km 1030 円で確定。残り 17 km を 240 円で進むことはできないので不適。
したがって、2300 円以下にはできないので、最も安い料金は 2310 円。
最後に、到着時の所持金について、100×(素数)-2310=10×(素数) の最小値を考える。
10×(素数) の十の位は 9 であるから、一の位が 9 である素数 19、29、59、… を考えると、最小値は 100×29-2310=10×59=590 (円)。
B-14. ひっくり返して足しましょう(tomh さん)
"算虎 5" で成績を残せなかった MD さんは、"算虎 6" を目前にして "算虎の穴" の特訓を受けていた。
「疲れたよぉ。今日はこれ位で……」
と、MD さんは講師のハルさんに懇願した。
「仕方ないなぁ。じゃ、算虎 6 想定問題を解いて終わりにしよう」
そう言って、ハルさんは問題を説明し始めた。
「3 桁の数を考えよう。もちろん、百の位は 0 じゃないよ。そして、その数を一の位から順にひっくり返すんだ。次に、元の数とひっくり返した数を足す。ここまでは、いいかな?」
MD さんが頷いたのを見て、ハルさんは続けた。
「足してできた数を見て、各桁がすべて偶数ならば、元の数を "偶数型" と呼ぼう。各桁がすべて奇数ならば、元の数を "奇数型"、そして、偶数と奇数が混ざっている場合は "混合型" としよう」
MD さんはノートにハルさんの言った言葉を書き留めた。
「この 3 桁の場合で例を挙げてみようか」
と言って、ハルさんは黒板に数字を書いた。
「例えば、341 から始めると、ひっくり返した数は 143 だから、341+143=484 となって、これは "偶数型" だ。724 は、ひっくり返して 427 だから、724+427=1151 で、"奇数型" だね。そして、970 の場合は、ひっくり返すと 079 となる。ひっくり返した数は、元の数より桁数が減っても構わないんだ。だから、970+79=1049 で、"混合型" となる。0 は偶数だよ。」
MD さんもハルさんの挙げた例をチェックした。MD さんの計算を待って、ハルさんは問題を出した。
「さて、じゃあ、3 桁の数 100~999 の中に、奇数型は何個あるかな?」
10 分程度経過した後、MD さんは答えを出した。
「3 桁では奇数型は 100 個になるね」
「おぉ、正しいね」
「じゃ、これで終わり?」
MD さんはホッとして言った。すると、ハルさんはニヤリとして応えた。
「算虎で、こんな簡単な問題が出るわけないじゃん。想定問題はこれからさ」
これを聞いて、MD さんは少し青ざめたが、ハルさんは構わず続けた。
「では、桁数を一気に増やします。13 桁にしたらどうなるかな?」
MD さんは、気が遠くなりそうだった……。
(この物語はフィクションです。実在の人物・団体とは一切関係ありません。(^^;)
というわけで、問題です。13 桁の場合、物語に出てきた手順を施して、奇数型になるのは何個ありますか。
〔解答・解説〕4 で割って 1 余るような桁数のときは、奇数型は存在しない。
これを 5 桁の場合で考えてみよう。
最初の 5 桁の数を □○▽△◇ とすると、ひっくり返した数は ◇△▽○□ である。
この 2 つの数を足した数のすべての桁が奇数になったとする。
ちょうど真ん中の桁(百の位)は ▽+▽ で、これは偶数であるから、下位(十の位)からのくり上がりがあり、1 が加わることになる。
もし、このくり上がりが、さらに下位(一の位)のくり上がりによるものならば、 △+○+1=10 を意味しており、十の位は 0、すなわち偶数になってしまう。
よって、△+○ は 10 以上の数であり、千の位の ○+△ もくり上がりを起こす。
この千の位のくり上がりを受けて、万の位は □+◇+1 となるが、これが奇数になるためには、□+◇ が偶数でなければならない。
ところが、一の位は ◇+□ であり、下位からのくり上がりがないので奇数である。
この矛盾は、2 つの数を足した数のすべての桁が奇数になったという仮定によるものである。
ゆえに、5 桁の数の中に奇数型は存在しない。
同様の議論で、13 桁の場合も奇数型は存在しないことがわかる。
すなわち、答えは 0 個。
C-15. 場合の数:席順(spicacoppe さん)
男子生徒が 5 人、女子生徒が 5 人います。
この 10 人の生徒が 1 列に並ぶとき、「どの 1 人をとっても、少なくとも右隣か左隣のどちらかに異性の生徒がいる」ような並び方は何通りありますか。
〔解答・解説〕一番左の 2 人と一番右の 2 人は、それぞれ互いに異性である。
すなわち、この条件を満たすのは以下の 4 通りであり、すべて互いに排反である。
1) 男女○○○○○○男女
2) 男女○○○○○○女男
3) 女男○○○○○○男女
4) 女男○○○○○○女男
1) の場合、男女の並び順は次の 11 通り。
男女どちらかが 3 人以上並ばないように樹形図を描いてゆけばよい。
最後の 2 つの○に男、男と入ったものについては、条件を満たさないので不適。
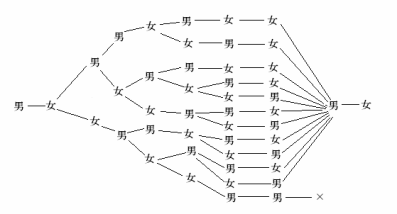
2) の場合は、1) の場合において、最後の 2 つの○に女、女と入ったものについては、条件を満たさないので不適であるから、10 通り。
3)、4) の場合は、1)、2) のそれぞれの場合の男女を入れかえればよい。
よって、1)~4) の場合をすべて合わせると (11+10)×2=42 (通り)。
ひとはすべて区別するから、求める場合の数は
42×(5×4×3×2×1)×(5×4×3×2×1)=604800 (通り)。
C-16. 一行お絵かき(rubik.cube さん)
下図において、右端のヒント(1 つ以上の数をコンマで区切ります)は連続して塗りつぶされるマス目の数を示します。コンマで区切られる数と数の間は 1 マス以上空きます。下図の例では、ヒント (5,2) を満たすパターンの数は 6 個です。
|
| (5,2) | ||||||||||
|
| |||||||||||
|
| |||||||||||
|
| |||||||||||
|
| |||||||||||
|
| |||||||||||
|
|
では、マス目が 10 個のとき、パターンの数が最大となるヒントに対するパターンの数はいくつですか。
〔解答・解説〕ヒントの数値が 2 以上の場合、塗りつぶされるマス目が連続し、その連続したマスが 1 マスのようにみなせるため、とりうる型の数は少なくなってしまう。
よって、とりうる型の数が最大となるヒントは (1)、(1,1)、(1,1,1)、(1,1,1,1)、(1,1,1,1,1) のいずれかである。
- (1) の場合:
とりうる型の数は 10 個。 - (1,1) の場合:
左側の黒マスを左端に置いたとき、右側の黒マスは 8 ヵ所のいずれかに置くことができる。
次に、左側の黒マスを 1 個右にずらして、左端から 2 番目に置くと、右側の黒マスは 7 ヵ所のいずれかに置くことができる。
このようにして、とりうる型の数は 8+7+6+5+4+3+2+1=36 (個)。 - (1,1,1) の場合:
最も左の黒マスを左端に置いたときは、8 マスにおける (1,1) の場合と同じであるから、とりうる型の数は 6+5+4+3+2+1=21 (個)。
次に、最も左の黒マスを1個右にずらして置いたときは、7 マスにおける (1,1) の場合と同じであるから、とりうる型の数は 5+4+3+2+1=15 (個)。
同様にして、(6+5+4+3+2+1)+(5+4+3+2+1)+(4+3+2+1)+(3+2+1)+(2+1)+1=56 (個)。 - (1,1,1,1) の場合:
最も左の黒マスを左端に置いたときは、8 マスにおける (1,1,1) の場合と同じであるから、(4+3+2+1)+(3+2+1)+(2+1)+1=20 (個)。
同様にして、{(4+3+2+1)+(3+2+1)+(2+1)+1}+{(3+2+1)+(2+1)+1}+{(2+1)+1}+1=35 (個)。 - (1,1,1,1,1) の場合:
とりうる型の数は 6 個。
以上により、とりうる型の数が最大となるのは、ヒントが (1,1,1) のときで 56 個。
別解(重複組合せ利用):
自由な空きマス(白点と呼ぶ)の配置に注目する。
- (1,1,1,1,1) の場合:
白点は 1 個で、それを配置できるのは、黒マスの間および外側の 6 ヵ所。
よって、とりうる型の数は 6 個。 - (1,1,1,1) の場合:
白点は 3 個で、それを配置できるのは 5 ヵ所。
よって、とりうる型の数は 5H3=7C3=35 (個)。 - (1,1,1) の場合:
白点は 5 個で、それを配置できるのは 4 ヵ所。
よって、とりうる型の数は 4H5=8C5=56 (個)。 - (1,1) の場合:
白点は 7 個で、それを配置できるのは 3 ヵ所。
よって、とりうる型の数は 3H7=9C7=36 (個)。
C-17. Taro くんが うまれたときの こわいゆめ(Taro さん)
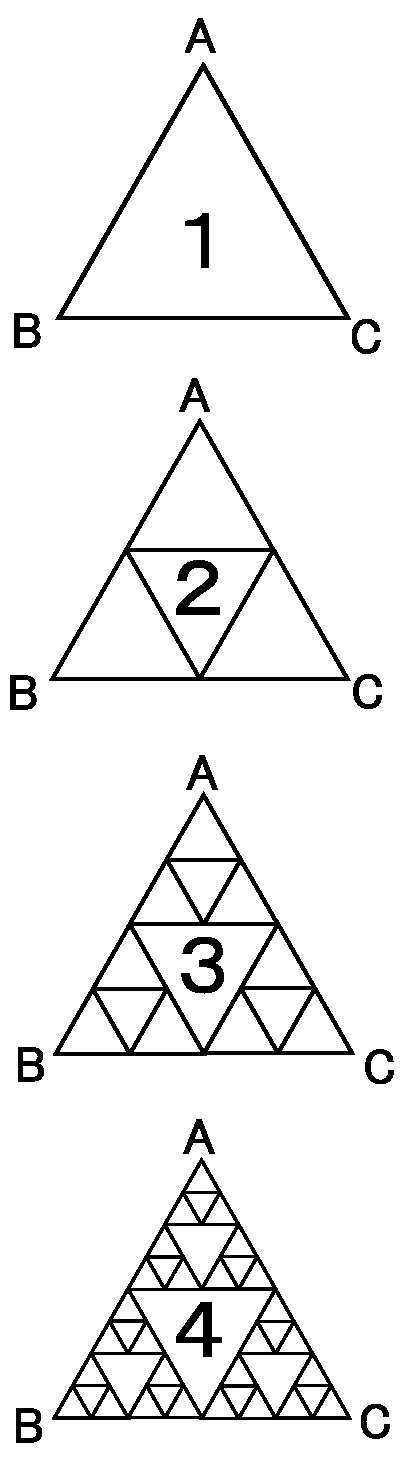
Taro くんがうまれて 1 日目、正三角形 ABC の形をした脳細胞が誕生しました。2 日目に、この脳細胞は合同な 4 つの正三角形型脳細胞に分裂しました。以後、1 日たつごとに、全ての脳細胞のうち、正三角形 ABC と辺を共有する脳細胞が合同な 4 つの正三角形型脳細胞に分裂していきました。
Taro くんはある日、その夢を思い出しました。そして、B から C に同じ点を 2 度通らないで行く方法が何通りあるか数えてみました。すると、1 日目は 2 通り、2 日目は ( X ) 通り、3 日目は ( Y ) 通り、4 日目は ( Z ) 通りでした。
では、( Z ) は ( Y ) の何倍ですか。
〔解答・解説〕辺 BC、CA、AB のまん中の点をそれぞれ D、E、F とする。
2 日目について、A を通らないものは (BDC)、(BDEC)、(BFDC)、(BFDEC)、(BFEC)、(BFEDC)、(BDFEC) の 7 通り。
また、A を通るものは (BFAEC)、(BFAEDC)、(BDFAEC) の 3 通り。
よって、X=7+3=10。
3 日目について、2 日目の図形を 3 つ組合わせたものと考える。
(三角形 AEF、三角形 FBD、三角形 EDC は 2 日目の三角形 ABC と同じ)
a) 三角形 AEF の辺を通らないもの(E、F は通ってもよい):
(7+3)×(7+3)=100 (通り)。
b) 三角形 AEF の辺を通るが、A を通らないもの:
B から F に行くときの三角形 FBD の通り方と、E から C に行くとき三角形 EDC の通り方は、D を同時に通らないので、合わせて (7+3)×(7+3)-3×3=91 (通り) あり、三角形 AEF の通り方は 7 通りあるから、{(7+3)×(7+3)-3×3}×7=637 (通り)。
c) 三角形 AEF の辺を通り、A を通るもの:
b と同様に考え、三角形 AEF の通り方は 3 通りあるから、{(7+3)×(7+3)-3×3}×3=273 (通り)。
よって、A を通らないもの (a、b) は (7+3)×(7+3)+{(7+3)×(7+3)-3×3}×7=737 (通り)。
A を通るもの (c) は {(7+3)×(7+3)-3×3}×3=273 (通り)。
したがって、Y=737+273=1010。
4 日目は、3 日目の三角形を用いて同様に考えると、a の場合が (737+273)×(737+273) 通りで、b、c の場合が {(737+273)×(737+273)-273×273}×(737+273) 通り。
したがって、Z=(737+273)×(737+273)+{(737+273)×(737+273)-273×273}×(737+273)。
ゆえに、Z÷Y=(737+273)+(737+273)×(737+273)-273×273=1010+1010×1010-273×273=946581。
C-18. 旗の色分け(川田 智之 さん)
良太くんと和子さんは、正方形を「田」の字型に 4 つに区分けした透明なフィルム材質の旗を、赤、黄、青、黒、茶の 5 色のうち 4 色を使って塗り分けます。ただし、区分けした 4 つの部分には、それぞれ異なる色を塗るものとします。また、回転させたり裏返したりして一致する場合は、同じ旗とみなします。例えば、以下の 3 つの旗はすべて同じ旗です。
|
|
|
では、良太くんが必ず赤と黄を使い、和子さんが必ず青と黒を使うとき、2 人がそれぞれ塗った旗が同じになる確率を求めてください。
〔解答・解説〕良太くんの旗の塗り方について考える。
赤と黄以外の青、黒、茶から 2 色を選ぶ方法は 3 通り。
また、特定の 4 色を使って塗る方法は 4×3×2×1÷4÷2=3 (通り)。
(÷4 は回転して一致する場合、÷2 は裏返して一致する場合を考えた)
よって、3×3=9 (通り) の塗り方がある。
同様にして、和子さんの旗の塗り方も 9 通りある。
2 人の塗り方が一致するのは、赤、黄、青、黒の 4 色で塗り分ける 3 通りのみであるから、求める確率は 3/(9×9)=1/27。
C-19. プレゼントの確率(タカピー さん)
A 君、B 君、C 君、D 君、E 君、F 君、G 君の 7 人が 1 人 1 つずつプレゼントを持ってきました。
ここに、1 つの大きな箱があります。まず、A 君、B 君、C 君の 3 人は持ってきたプレゼントを箱の中に入れました。次に、D 君は持ってきたプレゼントを箱の中に入れ、その箱の中からプレゼントを 1 つ取り出しました。そして、D 君と同じことを、E 君、F 君、G 君もこの順に続けて行いました。
では、A 君、B 君、C 君 の持ってきたプレゼントが 3 つとも、D 君、E 君、F 君、G 君のだれかによって取り出された確率を求めてください。
〔解答・解説〕箱の中に A 君(B 君、C 君)の持ってきたプレゼントが残っている確率は
(3/4)×(3/4)×(3/4)×(3/4)=81/256。
箱の中に A 君と B 君(A 君と C 君、B 君と C 君)の持ってきたプレゼントが残っている確率は (2/4)×(2/4)×(2/4)×(2/4)=16/256。
箱の中に A 君と B 君と C 君の持ってきたプレゼントが残っている確率は
(1/4)×(1/4)×(1/4)×(1/4)=1/256。
よって、箱の中に A 君、B 君、C 君の持ってきたプレゼントが少なくとも 1 つ残っている確率は (81/256)×3-(16/256)×3+1/256=49/64。
したがって、求める確率は 1-49/64=15/64。
C-20. ナベアツ君をアホにしないぞ(はなう さん)
ナベアツ君の前に、1~100 の番号が書かれたカードが 1 枚ずつ合計 100 枚あります。ここから、以下の〈ルール〉でカードを 1 枚ずつ取っていきます。
〈ルール〉
- はじめに 1 枚カードを取ります。(1 回目)
- 次に、1 回目に取ったカードの番号との差が 1 である番号が書いてあるカードの 1 つを取ります。(2 回目)
- 次に、2 回目に取ったカードの番号との差が 2 である番号が書いてあるカードの 1 つを取ります。(3 回目)
- 次に、3 回目に取ったカードの番号との差が 3 である番号が書いてあるカードの 1 つを取ります。(4 回目)
…… - K 回目は、K-1 回目に取ったカードの番号との差が K-1 である番号が書いてあるカードの 1 つを取ります。
- 1 度とったカードは 2 度と取れません。
- 取ることができるカードがなくなったら終了です。
さてここで、ナベアツ君はアホにならないために以下の〈追加ルール〉を設定しました。
〈追加ルール〉
- 3 の倍数と 3 が付く番号が書いてあるカードは取れません。
(12、13、15 などが取れないということです。)
以上のルールの下で、最も多くのカードを取ることができるのは 1 回目に取るカードが ( ア )のときで、そのとき取ることができるカードの枚数の最大は( イ )枚です。
( ア )、( イ )にあてはまる数を、この順にコンマ (,) で区切って答えてください。
〔解答・解説〕まず、3 の倍数でないときは、足し続けるか、引き続けることになることを示そう。
そこで、2 つの数 P、Q を 3 で割ったときの余りが等しいとき P≡Q と表し、x 枚目にとるカードを A(x) と表すことにする。
A(1)≡1 のとき:
1) A(1)-1≡0 より、A(2)≠A(1)-1。すなわち、A(2)=A(1)+1(≡2)。
2) A(2)-2≡0 より、A(3)≠A(2)-2。すなわち、A(3)=A(2)+2(≡1)。
3) A(3)-3=A(1) より、A(4)≠A(3)-3。すなわち、A(4)=A(3)+3(≡1)。
4) A(4)-1≡0 より、A(5)≠A(4)-1。すなわち、A(5)=A(4)+1(≡2)。
5) A(5)-2≡0 より、A(6)≠A(5)-2。すなわち、A(6)=A(5)+2(≡1)。
6) A(6)=A(5)+3(≡1) または A(6)=A(5)-3(≡1)。
以降は上記 4)~6) の繰り返しになる。
4)、5) のように、3 の倍数でないときは足し続けることがわかる。
同様にして、A(1)≡2 のとき、3 の倍数でないときは引き続けることがわかる。
次に、3 の倍数を連続して引く(足す)ことはできないことを示そう。
引く前の番号を□とすると、□-N+(N+1)+(N+2)-(N+3)=□ であるから、3 の倍数を連続して引くことはできない。足す場合も同様である。
では、具体的に考えていこう。
はじめに引いていく場合:
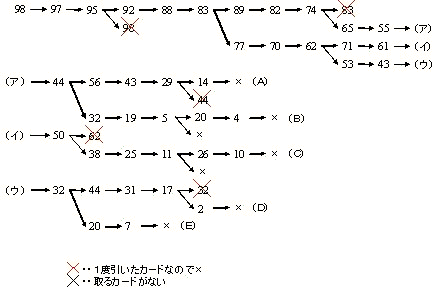
3 が付く番号も含めて書き出すと、図のようになる。
- 1 回目が 98 の場合:
6 回目が 83 となり、続けることができない。 - 1 回目が 95 の場合:
図の番号すべてから 3 を引いたものになる。
(ア)→ (B) のルートは 3 が付く番号が現れない。
このとき、取れるカードは 17 枚。 - 1 回目が 92 の場合:
図の番号すべてから 6 を引いたものになる。
(イ)→ (C) のルートで、32 が現れるまでの 12 枚が最多。 - 1 回目が 89 の場合:
図の番号すべてから 9 を引いたものになる。
4 回目が 83 となり、続けることができない。 - 1 枚目が 86 の場合:
図の番号すべてから 12 を引いたものなる。
(B)、(C) のルートとも、17 回目以降は 1 より小さくなる。
すなわち、取れるカードは 16 枚以下。
はじめに足していく場合:
- 1 回目が 1~29 の場合:
例えば、1 回目が 1 として書き出してみると、下図のように、必ず 30 台に達する(30 台となるないようにするためには、11 以上を足さなくてはならないが、その前に必ず 30 に達してしまう)。
取れるカードは最大 9 枚。
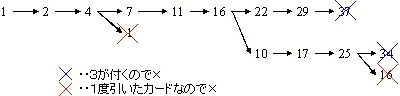
- 1 回目が 40 以上の場合:
はじめに引いていく場合(上図)、40~100 において取れるカードは最大 14 枚であるが、対称性を考えれば、足していく場合も同様に最大 14 枚。
よって、1 回目に 95 を取ったとき、最大 17 枚取ることができる。
C-21. 誰が誰やら(高橋 道広 さん)
A、B、C、D、E、F、G、H、I、J、K、L の 12 人の仲間が合宿をして、テニスのシングルスを総当たり戦で、1 日 6 試合 11 日間の日程で行いました。
最後の日は雨になって、対戦表の一部分が読めなくなってしまいました。
読めなくなった空欄のうち、ア~サにあてはまる選手名を、アイウエオ順にコンマで区切らず並べて答えてください。(例:ABCDEFGHIJK)
| 日 | 第1試合 | 第2試合 | 第3試合 | 第4試合 | 第5試合 | 第6試合 | ||||||
| 1 | A | I | D | H | B | C | ア | G | L | |||
| 2 | C | H | J | L | B | D | イ | G | I | |||
| 3 | A | L | F | H | B | E | ウ | G | K | |||
| 4 | B | I | F | J | A | C | エ | E | H | |||
| 5 | B | D | E | G | F | K | C | オ | J | L | ||
| 6 | B | C | E | H | F | G | カ | I | K | |||
| 7 | D | G | H | K | B | E | キ | J | L | |||
| 8 | E | J | G | I | D | H | ク | K | L | |||
| 9 | A | F | D | I | J | K | B | ケ | C | L | ||
| 10 | C | F | E | K | A | H | コ | J | L | |||
| 11 | A | C | D | E | G | サ | I | J | ||||
〔解答・解説〕対戦可能な相手を表にしてみる。太字は対戦の組み合わせが決定している相手、赤色は別の日に対戦することが決まっているため対戦できない相手を表している。
これにより対戦相手が決まる場合があり、他の相手とは対戦できないことにより決定する対戦相手を青色で表す。また、緑色はこの日以外には対戦できない相手を表す。
例えば、A は 7 日目以外には E と対戦できないので、この日は A と E が対戦する。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| A | I | BDGI | L | DGKL | CJL | FGIK | BEJL | DHKL | F | BDGI | C |
| B | EFJK | AEFK | CDIJ | I | D | C | ACFI | DHKL | EGH | AHJL | DEGIJ |
| C | EFJK | H | BEGK | DGKL | AHI | B | BEJL | DHKL | EGH | F | A |
| D | H | AEFK | BEGK | ACEH | B | FGIK | G | ABCF | I | AHJL | BFHKL |
| E | BCGL | BDGI | CDIJ | DGKL | G | H | ACFI | J | BCL | K | BFHKL |
| F | BCGL | BDGI | H | J | K | ADJL | BEJL | DHKL | A | C | DEGIJ |
| G | EFJK | AEFK | CDIJ | ACEH | E | ADJL | D | I | BCL | AHJL | BFHKL |
| H | D | C | F | DGKL | CJL | E | K | ABCF | BCL | BDGI | DEGIJ |
| I | A | AEFK | BEGK | B | CJL | ADJL | BEJL | G | D | AHJL | BFHKL |
| J | BCGL | L | BEGK | F | AHI | FGIK | ACFI | E | K | BDGI | BFHKL |
| K | BCGL | BDGI | CDIJ | ACEH | F | ADJL | H | ABCF | J | E | DEGIJ |
| L | EFJK | J | A | ACEH | AHI | FGIK | ACFI | ABCF | EGH | BDGI | DEGIJ |
対戦不可能な相手を表から削除し、青色と緑色の対戦相手を決定(黄色いセル)することにより、新たに対戦不可能なものが生じる。
このとき、同日に 2 試合はできないので、別の試合があって対戦不可能である相手をオレンジ色で表す。
するとまた、青色と緑色の対戦相手が決定する。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| A | I | BDG | L | DGK | J | GK | E | H | F | BDG | C |
| B | EFJK | AEFK | J | I | D | C | AF | HKL | EGH | AHJL | EGJ |
| C | EJK | H | EGK | DGKL | I | B | EJL | DKL | EG | F | A |
| D | H | AEFK | EK | ACE | B | FK | G | ACF | I | J | L |
| E | BCL | BDI | CDI | DL | G | H | A | J | BCL | K | BFL |
| F | BGL | BDGI | H | J | K | DL | BEL | DL | A | C | DEGI |
| G | FJK | AFK | CJ | ACH | E | AJL | D | I | BCL | AHJL | BFHKL |
| H | D | C | F | GL | JL | E | K | A | BL | BGI | GIJ |
| I | A | EFK | EK | B | C | JL | EJL | G | D | HJL | FHKL |
| J | BCG | L | B | F | A | GI | ACI | E | K | D | BH |
| K | BCGL | BDGI | CDI | AC | F | ADL | H | ABC | J | E | DGI |
| L | EFK | J | A | CEH | HI | FGIK | CFI | BCF | EGH | BDGI | D |
この作業をくり返す。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| A | I | BDG | L | DGK | J | GK | E | H | F | BG | C |
| B | EFK | AEFK | J | I | D | C | F | KL | EGH | AHL | EG |
| C | EJK | H | G | DGKL | I | B | JL | DKL | EG | F | A |
| D | H | AEFK | EK | ACE | B | FK | G | CF | I | J | L |
| E | BCL | BDI | CDI | DL | G | H | A | J | BCL | K | F |
| F | BGL | BDGI | H | J | K | DL | B | DL | A | C | E |
| G | FJK | AFK | C | ACH | E | AJL | D | I | BCL | AHJL | BFHK |
| H | D | C | F | GL | L | E | K | A | BL | BGI | J |
| I | A | EFK | EK | B | C | JL | JL | G | D | HL | FHK |
| J | CG | L | B | F | A | GI | CI | E | K | D | H |
| K | BCGL | BDGI | CDI | AC | F | ADL | H | BC | J | E | GI |
| L | EFK | J | A | CEH | H | FGIK | CFI | BCF | EGH | BGI | D |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| A | I | BDG | L | DGK | J | GK | E | H | F | BG | C |
| B | EK | AEK | J | I | D | C | F | KL | H | AHL | G |
| C | EJK | H | G | DKL | I | B | JL | DKL | E | F | A |
| D | H | AEFK | EK | ACE | B | FK | G | CF | I | J | L |
| E | BCL | BDI | DI | DL | G | H | A | J | C | K | F |
| F | GL | I | H | J | K | DL | B | DL | A | C | E |
| G | FJK | AFK | C | H | E | AJL | D | I | BL | AHJL | B |
| H | D | C | F | G | L | E | K | A | B | I | J |
| I | A | F | EK | B | C | JL | JL | G | D | H | K |
| J | CG | L | B | F | A | GI | CI | E | K | D | H |
| K | BCGL | BDGI | DI | AC | F | ADL | H | BC | J | E | I |
| L | EFK | J | A | CE | H | FGIK | CI | BCF | EG | BGI | D |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| A | I | BDG | L | DK | J | GK | E | H | F | BG | C |
| B | EK | AEK | J | I | D | C | F | KL | H | AL | G |
| C | JK | H | G | DKL | I | B | JL | DKL | E | F | A |
| D | H | AEK | K | ACE | B | FK | G | CF | I | J | L |
| E | BL | BD | I | DL | G | H | A | J | C | K | F |
| F | G | I | H | J | K | DL | B | DL | A | C | E |
| G | F | AK | C | H | E | AJL | D | I | L | AJL | B |
| H | D | C | F | G | L | E | K | A | B | I | J |
| I | A | F | E | B | C | JL | JL | G | D | H | K |
| J | CG | L | B | F | A | GI | CI | E | K | D | H |
| K | BCGL | BDG | D | AC | F | ADL | H | BC | J | E | I |
| L | EFK | J | A | CE | H | FGIK | CI | BCF | G | BG | D |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| A | I | BDG | L | DK | J | GK | E | H | F | BG | C |
| B | EK | AEK | J | I | D | C | F | KL | H | L | G |
| C | J | H | G | DKL | I | B | JL | DKL | E | F | A |
| D | H | AE | K | ACE | B | F | G | CF | I | J | L |
| E | BL | BD | I | DL | G | H | A | J | C | K | F |
| F | G | I | H | J | K | D | B | DL | A | C | E |
| G | F | K | C | H | E | J | D | I | L | AJ | B |
| H | D | C | F | G | L | E | K | A | B | I | J |
| I | A | F | E | B | C | JL | JL | G | D | H | K |
| J | C | L | B | F | A | G | CI | E | K | D | H |
| K | BCL | G | D | AC | F | ADL | H | BC | J | E | I |
| L | EK | J | A | CE | H | FIK | CI | BCF | G | B | D |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| A | I | B | L | DK | J | K | E | H | F | G | C |
| B | EK | A | J | I | D | C | F | K | H | L | G |
| C | J | H | G | DKL | I | B | L | D | E | F | A |
| D | H | AE | K | ACE | B | F | G | C | I | J | L |
| E | BL | BD | I | DL | G | H | A | J | C | K | F |
| F | G | I | H | J | K | D | B | L | A | C | E |
| G | F | K | C | H | E | J | D | I | L | A | B |
| H | D | C | F | G | L | E | K | A | B | I | J |
| I | A | F | E | B | C | L | J | G | D | H | K |
| J | C | L | B | F | A | G | I | E | K | D | H |
| K | BL | G | D | AC | F | A | H | B | J | E | I |
| L | EK | J | A | CE | H | I | C | F | G | B | D |
よって、組合せは次のように決まる。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| A | I | B | L | D | J | K | E | H | F | G | C |
| B | E | A | J | I | D | C | F | K | H | L | G |
| C | J | H | G | K | I | B | L | D | E | F | A |
| D | H | E | K | A | B | F | G | C | I | J | L |
| E | B | D | I | L | G | H | A | J | C | K | F |
| F | G | I | H | J | K | D | B | L | A | C | E |
| G | F | K | C | H | E | J | D | I | L | A | B |
| H | D | C | F | G | L | E | K | A | B | I | J |
| I | A | F | E | B | C | L | J | G | D | H | K |
| J | C | L | B | F | A | G | I | E | K | D | H |
| K | L | G | D | C | F | A | H | B | J | E | I |
| L | K | J | A | E | H | I | C | F | G | B | D |
| 日 | 第1試合 | 第2試合 | 第3試合 | 第4試合 | 第5試合 | 第6試合 | ||||||
| 1 | A | I | D | H | B | E | C | J | G | F | L | K |
| 2 | C | H | J | L | B | A | D | E | G | K | I | F |
| 3 | A | L | F | H | B | J | E | I | G | C | K | D |
| 4 | B | I | F | J | A | D | C | K | E | L | H | G |
| 5 | B | D | E | G | F | K | C | I | J | A | L | H |
| 6 | B | C | E | H | F | D | G | J | I | L | K | A |
| 7 | D | G | H | K | B | F | E | A | J | I | L | C |
| 8 | E | J | G | I | D | C | H | A | K | B | L | F |
| 9 | A | F | D | I | J | K | B | H | C | E | L | G |
| 10 | C | F | E | K | A | G | H | I | J | D | L | B |
| 11 | A | C | D | L | E | F | G | B | I | K | J | H |
したがって、答えは JEIKIJAAHIB。
C-22. ループ(ミキティ さん)
下のパズルを次のルールで解いたとき、あとの問いに答えてください。
〈ルール〉
- 点と点をタテヨコに線でつなげ、全体で 1 つのループ(輪っか)を作ります。
- 4 つの点 (+) で作られた小さな正方形の中の数字は、その正方形の辺に引く線の数です。
数字のない小さな正方形の辺には、何本の線を引くか分かりません。 - 線は交差したり、枝分かれしたりはしません。
| + | + | + | + | + | + | + | + | + | + | + | ||||||||||
| 1 | 0 | 1 | 1 | 1 | ||||||||||||||||
| + | + | + | + | + | + | + | + | + | + | + | ||||||||||
| 1 | 1 | 1 | ||||||||||||||||||
| + | + | + | + | + | + | + | + | + | + | + | ||||||||||
| 1 | 0 | 1 | ||||||||||||||||||
| + | + | + | + | + | + | + | + | + | + | + | ||||||||||
| 1 | 0 | 0 | 1 | 1 | 0 | |||||||||||||||
| + | + | + | + | + | + | + | + | + | + | + | ||||||||||
| 1 | 1 | 1 | ||||||||||||||||||
| + | + | + | + | + | + | + | + | + | + | + | ||||||||||
| 0 | 1 | 1 | ||||||||||||||||||
| + | + | + | + | + | + | + | + | + | + | + | ||||||||||
| 0 | 1 | 1 | 1 | 1 | 1 | |||||||||||||||
| + | + | + | + | + | + | + | + | + | + | + | ||||||||||
| 1 | 1 | 1 | ||||||||||||||||||
| + | + | + | + | + | + | + | + | + | + | + | ||||||||||
| 0 | 1 | 0 | ||||||||||||||||||
| + | + | + | + | + | + | + | + | + | + | + | ||||||||||
| 1 | 1 | 1 | 1 | 1 | ||||||||||||||||
| + | + | + | + | + | + | + | + | + | + | + |
ループの中に入る 0、1 はそれぞれ何個ありますか。順にコンマ (,) で区切って答えてください。
〔解答・解説〕線を引くところには -、線を引かないところには x と書くことにする。
0 の 3 辺に x をつける。
| + | + | x | + | + | + | + | + | + | + | + | + | |||||||||
| 1 | x | 0 | x | 1 | 1 | 1 | ||||||||||||||
| + | + | x | + | + | + | + | + | + | + | + | + | |||||||||
| 1 | 1 | 1 | ||||||||||||||||||
| + | + | + | + | + | + | x | + | + | + | + | + | |||||||||
| 1 | x | 0 | x | 1 | ||||||||||||||||
| + | + | x | + | + | x | + | + | x | + | + | + | + | x | + | ||||||
| 1 | x | 0 | x | x | 0 | x | 1 | 1 | x | 0 | x | |||||||||
| + | + | x | + | + | x | + | + | + | + | + | + | x | + | |||||||
| 1 | 1 | 1 | ||||||||||||||||||
| + | + | + | x | + | + | + | + | + | + | + | + | |||||||||
| x | 0 | x | 1 | 1 | ||||||||||||||||
| + | x | + | + | x | + | + | + | + | + | + | + | + | ||||||||
| x | 0 | x | 1 | 1 | 1 | 1 | 1 | |||||||||||||
| + | x | + | + | + | + | + | + | + | + | + | + | |||||||||
| 1 | 1 | 1 | ||||||||||||||||||
| + | x | + | + | + | + | + | + | x | + | + | + | + | ||||||||
| x | 0 | x | 1 | x | 0 | x | ||||||||||||||
| + | x | + | + | + | + | + | + | x | + | + | + | + | ||||||||
| 1 | 1 | 1 | 1 | 1 | ||||||||||||||||
| + | + | + | + | + | + | + | + | + | + | + |
斜めに 0-1 が隣り合うところに、2 つ x をつける。
左上の 1 については、さらに左上に 0 があると考え、1 の 2 つに x をつける。
他の 3 角も同様。
| + | x | + | x | + | x | + | x | + | + | + | + | + | - | + | x | + | ||||
| x | 1 | x | 0 | x | x | 1 | 1 | | | 1 | x | ||||||||||
| + | - | + | x | + | + | + | + | + | + | + | + | x | + | |||||||
| | | | | 1 | x | 1 | | | 1 | x | |||||||||||||
| + | + | + | - | + | + | + | x | + | x | + | + | + | x | + | ||||||
| x | 1 | x | x | 0 | x | 1 | x | |||||||||||||
| + | + | x | + | x | + | x | + | + | x | + | + | + | + | x | + | |||||
| 1 | x | 0 | x | x | 0 | x | 1 | 1 | x | 0 | x | |||||||||
| + | + | x | + | + | x | + | x | + | + | + | + | + | x | + | ||||||
| x | 1 | 1 | 1 | x | ||||||||||||||||
| + | + | + | x | + | + | + | + | + | + | + | + | |||||||||
| x | x | 0 | x | 1 | 1 | |||||||||||||||
| + | x | + | x | + | x | + | + | + | + | + | + | + | + | |||||||
| x | 0 | x | 1 | x | 1 | 1 | 1 | 1 | ||||||||||||
| + | x | + | - | + | + | + | + | + | + | + | + | + | ||||||||
| x | | | 1 | 1 | x | 1 | |||||||||||||||
| + | x | + | - | + | + | + | + | + | x | + | x | + | + | + | ||||||
| x | 0 | x | 1 | x | 0 | x | | | |||||||||||||
| + | x | + | - | + | + | + | + | + | x | + | + | + | - | + | ||||||
| x | 1 | | | 1 | 1 | 1 | x | 1 | x | ||||||||||||
| + | x | + | - | + | + | + | + | + | + | + | x | + | x | + |
左上、小さな輪を作らないよう、A、B にそれぞれ x をつける。
| + | x | + | x | + | x | + | x | + | - | + | - | + | + | + | - | + | x | + | ||
| x | 1 | x | 0 | x | x | 1 | | | 1 | | | 1 | x | |||||||||
| + | - | + | x | + | x | + | x | + | - | + | + | + | + | + | x | + | ||||
| | | | | x | x | 1 | x | x | 1 | | | 1 | x | ||||||||||
| + | A | + | - | + | - | + | - | + | + | x | + | x | + | + | + | x | + | |||
| | | x | x | 1 | x | x | 0 | x | 1 | x | |||||||||||
| + | B | + | x | + | x | + | x | + | + | x | + | + | + | + | x | + | ||||
| | | 1 | x | 0 | x | x | 0 | x | 1 | 1 | x | 0 | x | ||||||||
| + | x | + | x | + | - | + | x | + | x | + | + | + | + | + | x | + | ||||
| | | x | | | | | x | 1 | x | 1 | 1 | x | |||||||||||
| + | - | + | - | + | x | + | - | + | - | + | + | + | + | + | + | |||||
| x | x | x | 0 | x | 1 | x | 1 | |||||||||||||
| + | x | + | x | + | x | + | x | + | + | + | + | + | + | + | ||||||
| x | 0 | x | 1 | x | x | 1 | 1 | 1 | 1 | |||||||||||
| + | x | + | - | + | + | + | + | + | + | + | + | + | ||||||||
| x | | | 1 | 1 | x | 1 | |||||||||||||||
| + | x | + | - | + | + | + | + | + | x | + | x | + | + | + | ||||||
| x | 0 | x | 1 | x | 0 | x | | | |||||||||||||
| + | x | + | - | + | + | + | + | + | x | + | + | + | - | + | ||||||
| x | 1 | | | 1 | 1 | 1 | x | 1 | x | ||||||||||||
| + | x | + | - | + | + | + | + | + | + | + | x | + | x | + |
C には線を引けないので、C 下の 1 は右に、C 上の 1 は上に線を引ける。
| + | x | + | x | + | x | + | x | + | - | + | - | + | - | + | - | + | - | + | x | + |
| x | 1 | x | 0 | x | x | 1 | | | x | x | 1 | x | x | | | 1 | x | |||||
| + | - | + | x | + | x | + | x | + | - | + | x | + | C | + | - | + | x | + | x | + |
| | | | | x | x | 1 | x | | | x | 1 | | | | | | | 1 | x | |||||||
| + | x | + | - | + | - | + | - | + | - | + | x | + | x | + | x | + | - | + | x | + |
| | | x | x | 1 | x | x | x | 0 | x | | | 1 | x | x | x | |||||||
| + | x | + | x | + | x | + | x | + | x | + | x | + | - | + | x | + | x | + | x | + |
| | | 1 | x | 0 | x | x | 0 | x | x | 1 | | | x | x | 1 | x | 0 | x | ||||
| + | x | + | x | + | - | + | x | + | x | + | x | + | + | + | - | + | x | + | ||
| | | x | | | | | x | 1 | x | 1 | 1 | | | x | ||||||||||
| + | - | + | - | + | x | + | - | + | - | + | + | + | + | + | + | |||||
| x | x | x | 0 | x | 1 | x | 1 | |||||||||||||
| + | x | + | x | + | x | + | x | + | + | + | + | + | + | + | ||||||
| x | 0 | x | 1 | x | x | 1 | 1 | 1 | 1 | |||||||||||
| + | x | + | - | + | + | + | + | + | + | + | + | + | ||||||||
| x | | | 1 | 1 | x | 1 | |||||||||||||||
| + | x | + | - | + | + | + | + | + | x | + | x | + | + | + | ||||||
| x | 0 | x | 1 | x | 0 | x | | | |||||||||||||
| + | x | + | - | + | + | + | + | + | x | + | + | + | - | + | ||||||
| x | 1 | | | 1 | 1 | 1 | x | 1 | x | ||||||||||||
| + | x | + | - | + | + | + | + | + | + | + | x | + | x | + |
左下、小さな輪を作らないよう、D、E にそれぞれ x をつける。
| + | x | + | x | + | x | + | x | + | - | + | - | + | - | + | - | + | - | + | x | + |
| x | 1 | x | 0 | x | x | 1 | | | x | x | 1 | x | x | | | 1 | x | |||||
| + | - | + | x | + | x | + | x | + | - | + | x | + | C | + | - | + | x | + | x | + |
| | | | | x | x | 1 | x | | | x | 1 | | | | | | | 1 | x | |||||||
| + | x | + | - | + | - | + | - | + | - | + | x | + | x | + | x | + | - | + | x | + |
| | | x | x | 1 | x | x | x | 0 | x | | | 1 | x | x | x | |||||||
| + | x | + | x | + | x | + | x | + | x | + | x | + | - | + | x | + | x | + | x | + |
| | | 1 | x | 0 | x | x | 0 | x | x | 1 | | | x | x | 1 | x | 0 | x | ||||
| + | x | + | x | + | - | + | x | + | x | + | x | + | - | + | - | + | - | + | x | + |
| | | x | | | | | x | 1 | x | x | 1 | x | 1 | x | | | x | |||||||
| + | - | + | - | + | x | + | - | + | - | + | x | + | x | + | x | + | + | + | ||
| x | x | x | 0 | x | 1 | x | | | 1 | x | |||||||||||
| + | x | + | x | + | x | + | x | + | x | + | x | + | x | + | + | + | + | |||
| x | 0 | x | 1 | x | x | x | 1 | | | x | 1 | 1 | 1 | ||||||||
| + | x | + | - | + | - | + | - | + | x | + | - | + | + | + | + | + | ||||
| x | | | D | 1 | x | | | 1 | x | x | 1 | |||||||||||
| + | x | + | - | + | x | + | x | + | x | + | + | x | + | x | + | + | + | |||
| x | 0 | x | | | x | 1 | | | x | 0 | x | | | ||||||||||
| + | x | + | - | + | x | + | x | + | - | + | + | x | + | + | + | - | + | |||
| x | 1 | | | E | x | 1 | x | 1 | 1 | x | 1 | x | |||||||||
| + | x | + | - | + | - | + | - | + | - | + | + | + | + | x | + | x | + |
左下、中くらいの輪を作らないよう、F に x をつける。
| + | x | + | x | + | x | + | x | + | - | + | - | + | - | + | - | + | - | + | x | + |
| x | 1 | x | 0 | x | x | 1 | | | x | x | 1 | x | x | | | 1 | x | |||||
| + | - | + | x | + | x | + | x | + | - | + | x | + | C | + | - | + | x | + | x | + |
| | | | | x | x | 1 | x | | | x | 1 | | | | | | | 1 | x | |||||||
| + | x | + | - | + | - | + | - | + | - | + | x | + | x | + | x | + | - | + | x | + |
| | | x | x | 1 | x | x | x | 0 | x | | | 1 | x | x | x | |||||||
| + | x | + | x | + | x | + | x | + | x | + | x | + | - | + | x | + | x | + | x | + |
| | | 1 | x | 0 | x | x | 0 | x | x | 1 | | | x | x | 1 | x | 0 | x | ||||
| + | x | + | x | + | - | + | x | + | x | + | x | + | - | + | - | + | - | + | x | + |
| | | x | | | | | x | 1 | x | x | 1 | x | 1 | x | | | x | |||||||
| + | - | + | - | + | x | + | - | + | - | + | x | + | x | + | x | + | - | + | x | + |
| x | x | x | 0 | x | 1 | x | | | 1 | x | x | | | x | x | |||||||
| + | x | + | x | + | x | + | x | + | x | + | x | + | x | + | - | + | x | + | x | + |
| x | 0 | x | 1 | x | x | x | 1 | | | x | 1 | | | x | 1 | x | 1 | x | ||||
| + | x | + | - | + | - | + | - | + | x | + | - | + | x | + | - | + | - | + | - | + |
| x | | | x | 1 | x | | | 1 | x | | | x | 1 | x | x | | | |||||||
| + | x | + | - | + | x | + | x | + | x | + | - | + | x | + | x | + | - | + | x | + |
| x | 0 | x | | | x | 1 | | | | | x | 0 | x | | | | | | | |||||||
| + | x | + | - | + | x | + | x | + | - | + | F | + | x | + | x | + | x | + | - | + |
| x | 1 | | | x | x | 1 | x | F | 1 | x | | | 1 | x | 1 | x | ||||||
| + | x | + | - | + | - | + | - | + | - | + | - | + | - | + | - | + | x | + | x | + |
よって、ループの中に入る 0、1 の個数はそれぞれ 4、15。
