A-01. 板を塗りつぶす(だいすけ さん)
縦 1.4 m、横 2 m の長方形の板があります。いま、この板の片面の対角線の交点にヒモの一端をつけ、ヒモのもう一端にはチョークを結びました。では、このチョークで板の両面をすべて塗りつぶすために必要なヒモの長さは最短で何 cm ですか。ただし、板の厚みやチョークの大きさ、チョークを結ぶのに要するヒモの長さは考えないものとします。
〔解答〕149 (cm)
A-02. ラーメンのどんぶりを眺めながら考えた(おかひで博士 さん)
東西方向(横)が南北方向(縦)よりも長く、縦の長さが 2 m 以上の長方形の土地があります。土地の縦、横の長さはメートル単位で整数で、土地には外周を含めて 1 m 間隔で格子状にラインが引いてあります。ラインが交わる点(外周にある角や丁字路も含む)を交差点とよぶことにします。
A 君は次の規則でライン上を進みます:
- まず、外周にない交差点(十字路)を 1 つ選び、そこを出発点として東に何 m か進み、右に曲がります。
- そして、1 m 進むたびに右を見て、1 m 先の交差点を通ったことがある(出発した交差点を含む)ときは、曲がらずにそのまままっすぐ 1 m 進み、通ったことがないときは、右に曲がり 1 m 進みます。これを繰り返していき、進めなくなったところで止まります。
ここで、規則 1 における出発点の選び方や、東に何 m 進むかは、その土地で進む道のりが最も長くなるように決めます。下の図は、縦 3 m、横 4 m の長方形の土地を進んだ一例を表しており、このとき進んだ道のりは 19 m です。
さて、A 君がある長方形の土地において進んだ道のりは 2222 m でした。このとき、土地の縦、横の長さの組合せは何通りありますか。
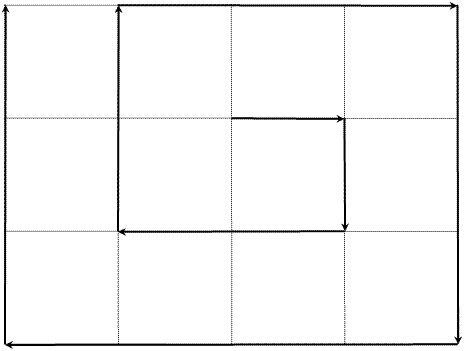
〔解答〕5 (通り)
A-03. 凹五角形の面積は(川田 智之 さん)
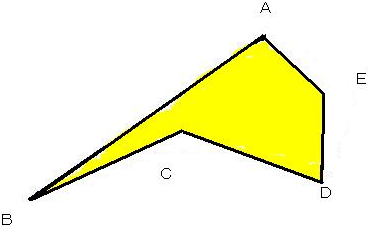
図のような、BC=CD=1 cm、AE=DE、角 B=15°、角 C=210°、角 D=45°、角 E=150° である凹五角形 ABCDE の面積は何 cm² ですか。
〔解答〕0.5 (cm²)
A-04. いい加減な四角形(ごんごんま さん)
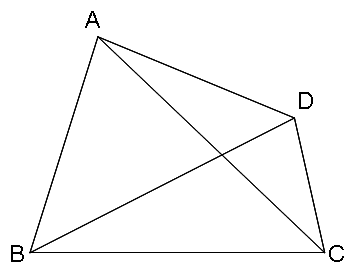
図のような四角形 ABCD において、
角 ABD=角 ACB=角 CBD×2=角 ACD×2=角 CAD×4
という関係が成り立っています。このとき、角 BAD の大きさは何度ですか。
ただし、図は必ずしも正確ではありません。
〔解答〕450/7 (度)
A-05. 天下は伊豆にあり(CRYING DOLPHIN さん)
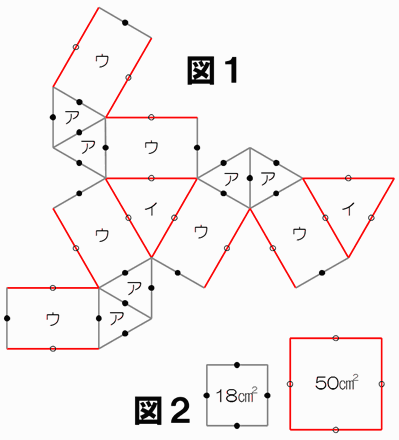
図 1 はある(へこみのない)立体の展開図で、面は次の 3 種類からなります:
ア…正三角形(小)、イ…正三角形(大)、ウ…長方形
ここで、同じ色、同じ印をつけた辺の長さは等しいです。また、図 2 は図 1 の立体に使われた辺と等しい長さの辺で正方形をつくったもので、その面積は 18 cm² と 50 cm² です。
では、図 1 の展開図を組み立ててできる(へこみのない)立体の体積は何 cm³ ですか。
〔解答〕348 (cm³)
B-06. 11 の倍数(hide さん)
1 以上 1 億以下の整数のうち、110、121 のように、どの位の数も 0、1、2 のいずれかである 11 の倍数は何個ありますか。
〔解答〕1106 (個)
B-07. 1800 枚のカード(長野 美光 さん)
A、B 2 つの箱があります。A の箱には 1 から 1800 までの整数が 1 つずつ記された 1800 枚のカードが入っています。B の箱には何も入っていません。
次の 5 つの操作をこの順に行います:
〔操作 1〕A の箱の中の 2 の倍数が記されたカードを B の箱に移す。
〔操作 2〕B の箱の中の 3 の倍数が記されたカードを A の箱に移す。
〔操作 3〕A の箱の中の 4 の倍数が記されたカードを B の箱に移す。
〔操作 4〕B の箱の中の 5 の倍数が記されたカードを A の箱に移す。
〔操作 5〕A の箱の中の 6 の倍数が記されたカードを B の箱に移す。
〔操作 5〕のあと、 A の箱に入っているカードを、記された数の小さい順に並べ、一番小さい数が上になるように山をつくります。そして、この山に対して次のような操作をします:
一番上のカードを捨て、次(上から 2 番目)のカードを山の一番下に移す。
以下同様に、1 枚捨て、1 枚山の下に移すという操作を繰り返す。
では、最後に残ったカードに記されている数は何ですか。
〔解答〕1791
B-08. いっしょに出発進行!(ぶぶおパパ さん)
ある駅には南北線、東西線、海岸線の 3 つの地下鉄線が通っています。電車の発車間隔はそれぞれの路線で一定ですが、それぞれ異なります。始発はどれも午前 6 時 37 分発で、午前 7 時までにどの路線でもそれぞれ 2 本目の電車が発車します。そして、終発の 1 本手前の電車はどの路線でも午後 11 時 15 分よりも前に発車し、終発はどれも午後 11 時 25 分発です。どの路線でも電車の発車時刻は分単位(○時○分ちょうど)で、3 つの路線で電車が同時に発車することは、始発と終発を含めて 1 日に 4 回あります。
では、2 つ以上の路線で電車が同時に発車することは 1 日に何回ありますか。考えられる回数が複数ある場合は、小さい順にコンマで区切って答えてください。
〔解答〕31,37 (回)
B-09. 表を埋める問題。(君の船 さん)
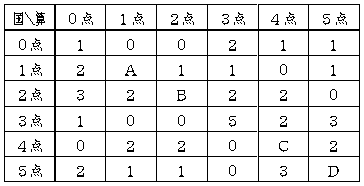
表は、何人かの小学生が国語と算数のそれぞれ 5 点満点のテストを受けた結果をまとめたものです。例えば、国語が 2 点で算数が 1 点の生徒は 2 人いることを表しています。
国語と算数の平均点はそれぞれ 2.7 点、2.6 点でした。このとき、A、B、C、D に当てはまる人数の組合せとして考えられるものをすべて求め、A、B、C、D をそれぞれ千の位、百の位、十の位、一の位とする 4 けたの数(上位けたが 0 のときは 0 で埋め、形式的に 4 けたとする)に変換し、小さい順にコンマで区切って答えてください。例えば、(A,B,C,D)=(0,0,0,1),(0,0,1,0),(0,1,0,0),(1,0,0,0) の場合は『0001,0010,0100,1000』と答えてください。
〔解答〕0430,0502,1321,2140,2212,3031,3103
B-10. 分かりません。分かりました。(正7角形 さん)
以下は先生と 3 人の生徒 A、B、C の会話です。先生の好きな数を答えてください。
ただし、先生も生徒も十分賢く、ウソはつかないものとします。
先生「ぼくの好きな数を当ててください。その数はただ一つで、1 以上 80 以下の整数です。これから、A 君には 9 で割ったあまりを、B 君には 7 で割ったあまりを、C 君には約数の個数を教えます。」
(教える)
先生「ぼくの好きな数は分かりましたか。」
A、B、C(同時)「分かりません。」
先生「ではヒントを出しましょう。その数は偶数です。C 君は約数の個数を聞いて、気づいていたと思います。」
C「はい。」
先生「ぼくの好きな数は分かりましたか。」
A「分かりません。」
B「分かりません。」
C「分かりません。」
B「分かりました。」
〔解答〕30
B-11. 少し早いバレンタイン(ハルカ さん)
214214214 人の男の子と 214214214 人の女の子が輪になって並んでいます。ハルカさんは男の子全員にチョコレートをプレゼントしたいと思っています。
ハルカさんはこの 428428428 人の中から 1 人を選び、その人から順に時計回りに話しかけながら 1 周します。女の子に話しかけたとき、ハルカさんは「友チョコ」としてチョコレートを 1 つもらえ、男の子に話しかけたとき、ハルカさんはチョコレート(他の女の子からもらったものも含みます)を 1 つ手渡します。このようにすると、男の子が何人も連続したとき、女の子からもらったチョコレートでは足りなくなることが予想されますので、それに備えてハルカさんは自分でチョコレートを何個か(0 個~214214214 個)用意しようと考えています。そこで、ハルカさんは 428428428 人の輪をよく見て、自分で用意しなければならないチョコレートの数が最も少なくなるように、最初に話しかける人を決めます。
では、ハルカさんが自分で用意しなければならないチョコレートは何個ですか。男の子と女の子の並び方は何通りもありますが、考えられる個数のうち最大の数を答えてください。
〔解答〕0 (個)
C-12. 8 回大会なので 8 を使った問題(abcba@jugglermoka さん)
次のような、3 つの 3 けたの整数「アイウ」、「エオイ」、「イカア」と、演算子記号□が不明な式があります:
アイウ□エオイ=イカア
ここで、ア~カには 0~9 の数字のいずれかが対応し、異なる記号に同じ数字が入ってもよいですが、3 けたの整数であることから、ア、エ、イは 0 ではありません。また、ア、イのうち少なくとも一方は 8 で、演算子記号□は+、-、×、÷のいずれかです。
では、(ア,イ,ウ,エ,オ,カ,□)の組合せは何通りありますか。
〔解答〕136 (通り)
C-13. すれ違いの人生(Mさん さん)
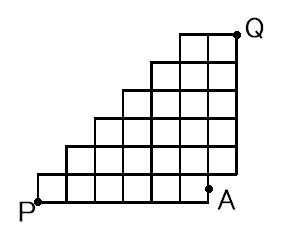
図のような等間隔で曲がり角のある道路があります。ゴローくんは P 地点から Q 地点まで、トシヤくんは Q 地点から P 地点まで、この道路を通って遠回りをすることなく向かいます。2 人は同時に出発し、同じ速さでお互いの目的地に向かい、同時に目的地に到着します。
では、2 人が目的地に到着するまでの道順のうち、途中で 2 人がすれ違うようなものは何通りありますか。ただし、例えば A 地点ですれ違う場合でも、目的地までの 2 人の道順が異なるものは別に数えます。
〔解答〕210920 (通り)
C-14. ジャングルジム II(ゲーム 10 種ランキング戦 さん)
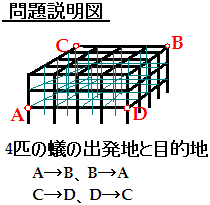
図のような、立方体を 4×4×2 の直方体状に積み重ねた形のジャングルジムがあります。いま、4 匹のアリがそれぞれの目的地へ向かってスタートしました。4 匹のアリはすべて同じ速さで、最短経路を通ってそれぞれの目的地へ向かいます。最短経路が複数あるときは、そのうちの一つを無作為に選んで通ります。
では、途中で 3 匹以上のアリが一同に会する確率はいくつですか。
〔解答〕5168/64827 または 3747995/258280326
C-15. ワープマシーン!(ぽっぽ さん)
辺 AB、AD の長さが 100 m、辺 AE の長さが 200 m の直方体 ABCD-EFGH があり、辺 AE、BF、CG、DH の真ん中の点をそれぞれ I、J、K、L とします。これら 12 個の点 A~L の上にワープマシーンが置かれてあり、以下の条件のいずれかを満たすときに限り、X から Y へワープすることができます。ここで、X、Y は A~L のいずれかの点とします。
- XY 間がちょうど 100 m であり、X、Y の少なくとも一方が直方体の 8 つの頂点 A~H のいずれかである。
- XY が AF、AH、AJ、AK、AL、BE、BI、BL、CF、CI、CJ、DJ のいずれかに平行、または一致する。
では、A を出発して、ワープマシーンだけを使い、A を除く 11 個の点 B~L を 1 回ずつ経由し、再び A にもどってくる方法(例:A→B→I→C→D→J→E→F→K→G→H→L→A)は何通りありますか。
〔解答〕926208 (通り)
C-16. GOOOOOL っ!!(ほげ さん)〔出題ミスのため参考掲載〕
サッカーの PK 戦を 7 人で行います。先攻 A チーム、後攻 J チームが最大で 7 回、交互にボールを蹴り(試技という)、ゴール成功数の多いチームを勝ちとします。ただし、各回の試技は先攻 A チームが行ったら、必ず後攻 J チームも行い、7 回までに勝敗が決まらなかった場合は引き分けとします。ゴール成功を○、失敗を×で表すとき、次の 2 つの条件をともに満たす○×の表記方法(※)は何通りありますか。〔下線部を追記〕
- 途中、自分チームのゴール成功数が相手チームのゴール成功数を上回らないことが分かった時点で試合は終了する。
- J チームは一度だけ A チームにリードされるが、最後は J チームのゴール成功により勝つ。
(※)表記方法の例:
| ○ | ○ | × | × | × | × |
| × | ○ | × | ○ | ○ | ○ |
という表記においては、6 回目の J チームのゴール成功により、A チームのゴール成功数は 4 を上回らないことから、条件 1 により試合は終了します。また、1 回目の A チームのゴール成功の時点で J チームはリードされたとみなします(1 回目の J チームの試技の前に判定する)。そして、最後は J チームのゴール成功により J チームが勝ったので、条件 2 を満たします。よって、この表記方法は答えのうちの 1 通りとなります。
C-17. フィールドアスレチック(なか さん)

あるフィールドアスレチックに、一列に並んだ切り株の上を進んで行く「切り株渡り」というポイントがあります。切り株は図のように高い切り株から始まり、高低交互に 24 本並んでいます。危ないのでもどってはいけません。
ジャンプが得意なマサル君は、高い切り株からは最大で 3 本先まで飛べますが、低い切り株からは次の切り株にしか行けないそうです。例えば、1 本目から 5 本目まで進む場合の数(踏む切り株の番号)は次のように 5 通りあります:
- 1 - 2 - 3 - 4 - 5
- 1 - 2 - 3 - 5
- 1 - 3 - 4 - 5
- 1 - 3 - 5
- 1 - 4 - 5
では、マサルさんが 1 本目から 23 本目まで進む場合の数を(ア)通り、1 本目から 24 本目まで進む場合の数を(イ)通りとするとき、(イ)÷(ア)の値を小数(分数は不可)で答えてください。ただし、小数第 9 位以下がある場合は、小数第 9 位を四捨五入して小数第 8 位まで答えてください。
〔解答〕1.41421356
